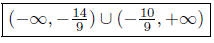Solving Equations & Inequalities

7.19. Solution: Using the Method of Signs we can easily solve the
inequality w⁴ − 15w ≥ 0 in exactly the same way we did in Exercise
7.18. Thus,
w⁴ − 15w ≥ 0 has solution w ≤ 0 or w ≥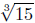

To continue the analysis, we need to break our argument down into
cases.

Case 1. w ≥ 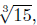in particular w is positive.
Since w > 0, w⁴ − 15w < w⁴. Take the square root of both sides we
get 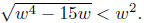This implies that

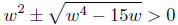
since we are adding/subtracting a smaller number. But this means,

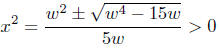
since both numerator and denominator are positive.

Case 2. w ≤ 0. Actually, w ≠0 since w appears in the denominator.
Since w < 0, w⁴ < w⁴−15w, since we are subtracting a negative number,
the result will be larger. Taking roots, we get
Therefore,

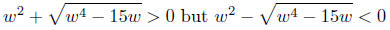
This means,


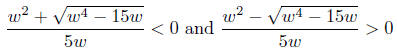
since, you’ll recall, we are assuming in this case that w < 0.

Summary.
1. For any w ≥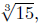


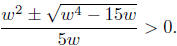
In this case, there are four solutions for x.

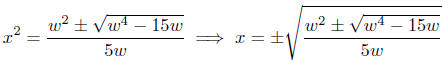
Ouch!

2. For any w < 0, only

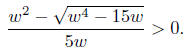
In this case, there are two solutions for x.

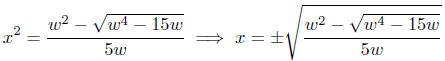
That was ugly!

7.20. Solutions:
(a) Solve for x: |x + 3| < 8.

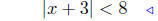	given
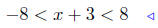	from (16)
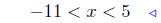	add −3 to all sides

Presentation of Solution:

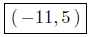
(b) Solve for x: |4x + 9| ≤ 1.
 

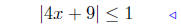	given
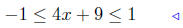	from (16)
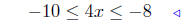	add −9 to all sides
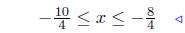	multiply all sides by 1/4

Now, reducing to lowest terms we get the . . .
Presentation of Solution: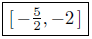

(c) Solve for x: |2 − 7x| ≤ 3.
 

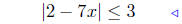	given
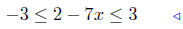	from (16)
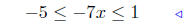	add −2 to all sides
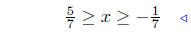	multiply all sides by −1/7

or

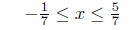
In the last step we have multiplied both sides by a negative
number, this will reverse the direction of the inequality!
Presentation of Solution:

7.21. Solution to (a) Solve for x: |9x − 2| ≥ 3.
|9x − 2| ≥ 3
Use (17) to split the inequality!
 

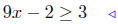	upper inequality		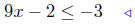lower inequality
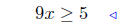	add 2 both sides		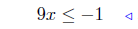add 2 both sides
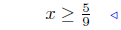	divide by 9		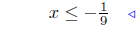divide by 9
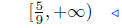	solution set		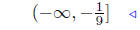solution set

Now, join the solutions!
Solution Set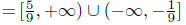
Presentation of Solution:

Solution to (b) Solve for x: |2 − 3x| > 6.
|2 − 3x| > 6

Use (17) to split the inequality!
 

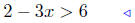	upper inequality		lower inequality
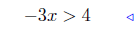	add −2		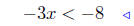add −2
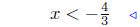	divide by −3		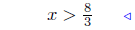divide by 5
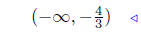	solution set		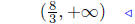solution set

Now, join the solutions!
Solution Set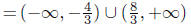
Presentation of Solution: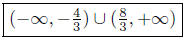

Comment: Hopefully, you understand when to include the endpoints
and when not to include them in your solution set, and, most importantly,
how do denote the inclusion/exclusion of the endpoints.

Solution to (c) Solve for x: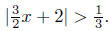

Use (17) to split the inequality!
 

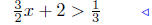	upper inequality		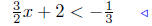lower inequality
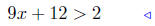	multiply by 6		multiply by 6
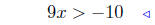	add −12		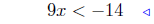add −12
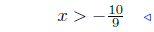	divide by 9		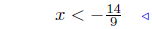divide by 9
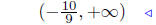	solution set		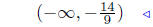solution set

Now, join the solutions!
Solution Set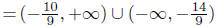
Presentation of Solution: