Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

A catalog of essential functions

Linear functions (graph is line) f(x) = mx + b

Polynomials

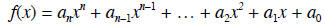
where n is a nonnegative integer

coefficients degree

linear when degree is 1 (graph is line)
quadratic when degree is 2 (graph is parabola)
cubic when degree is 3

Power functions

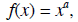where a is a constant

a = n is a positive integer (have a polynomial in this case)
a = 1 a = 2 a = 3 a = 4

a = 1/n, where n is a positive integer

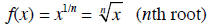
a = 1/2 a = 1/3

a = –1 f(x) = 1/x

Rational functions

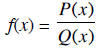
where P(x) and Q(x) are polynomials

Trigonometric Functions

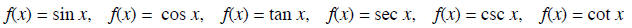
Exponential functions and logarithms a is a positive constant, a ≠ 1

exponential function

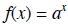
domain range

logarithm

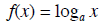
domain range

TRANSFORMATIONS of functions (for graphing)

Shifts c > 0
y = f(x) + c shifts the graph of y = f(x) up by c units
y = f(x) – c shifts the graph of y = f(x)
y = f(x – c) shifts the graph of y = f(x)
y = f(x + c) shifts the graph of y = f(x)

Stretching and Compressing c > 1
y = cf(x) stretches the graph of y = f(x) vertically by a factor of c
y = (1/c)f(x) compresses the graph of y = f(x) vertically by a factor of c
y = f(cx) compresses the graph of y = f(x) by a factor of c
y = f(x/c) stretches the graph of y = f(x) by a factor of c

Reflecting
y = –f(x) reflects the graph of y = f(x) through the
y = f(–x) reflects the graph of y = f(x) through the

EXAMPLE Graph

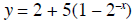
Combining functions

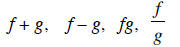
EXAMPLE For 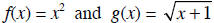, find rules for each of 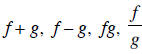. Also specify
the domain of each.

domain of f is domain of g is

	domain

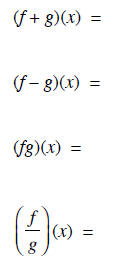Composition of functions For two functions f and g, the composition 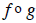of f with g is
defined by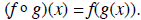

Domain of 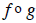consists of the numbers x that are in the domain of g AND such that g(x) is
in the domain of f.

EXAMPLE For f(x) = cos x and 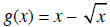, find

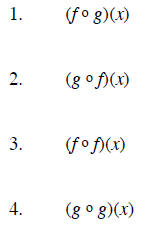
RECALL Trig identities and unit circle