Quadratic Function

DEFINITION.
A quadratic function is a polynomial of degree 2:



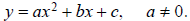
The graph is a parabola.
• If a > 0, the horns point up.

• If a < 0, the horns point down.

•If |a| > 1, the parabola is narrower than y = x².

• If |a| < 1, the parabola is wider than y = x².

Determine the shape of the following graphs. Pick the
shape below.

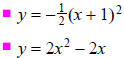
Given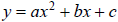
Get the roots by factoring or using the quadratic formula:
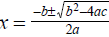. No roots if

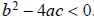
COMPLETING THE SQUARE THEOREM. Every quadratic
function may be written in the form:



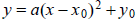
where 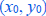is the vertex (or nose) of the parabola.

Proof. Given

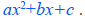
• Factor the a out of the ax²+bx part.

• Divide the new coefficient of x by 2 and square.
Add this to complete the square.

• Anything which is added must also be subtracted to
preserve equality.

• Find the roots (the roots are the x-intercepts).

• Write in completed square form:

• Graph. On the graph list both coordinates of the vertex.


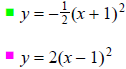
Find the vertex.

Find the graph with the correct shape and position.

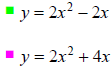
Find the roots. x = ?, ?
Write equation in the form: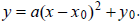

Find the vertex.
 

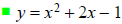
WORD PROBLEMS

• Draw the picture. Indicate the variables in the picture.
• Write the given equations which relate the variables.
• Solve for the wanted quantities.

The perimeter of a rectangle is 10 feet.
Express the area A in terms of the width x.

The area of a rectangle is 10 square feet.
Express the perimeter P in terms of the width x.

List the given.

Write the perimeter as a function of x

The corner of a triangle lies on the line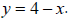

Express the triangle’s area and perimeter in terms of the
base x.

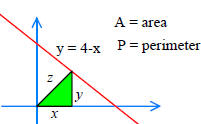
The area of an isosceles triangle is 16.

Write the triangle’s height h in terms of its width w.

Write the triangle’s width w in terms of its height h.

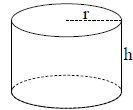
The curved surface
area is the area of the
can’s side, excluding
the top and bottom

The height of a can (right circular cylinder)
is three times the radius.
Express the radius as a function
of the curved surface area.

The height of a can (right circular cylinder)
is four times the radius.
Express the curved surface area as a function
of the radius.