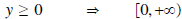Inverse Functions

Finding The Inverse of a Function

In the beginning of this section when we defined functions by giving a table of data we found the inverse by
interchanging the two columns of data.

If a function is described by an expression, to find the rule that defines a function’s inverse we interchange the
x’s and the y’s in the expression, and then solve for y. For the inverse to be a function we must guarantee that
the original function is one-to-one.

Example 1: Find f^-1 for 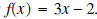Verify your results using the property of inverse functions.
Support your conclusion graphically.
Solution:

We know that the graph of the line 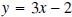passes the horizontal line test , and is therefore a
one-to-one function. To prove that f is one-to-one algebraically, we use the definition of one-to-one to
show that 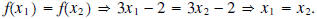Therefore, f is one-to-one.
Write the function as
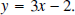
Interchange the x and the y:
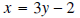
Solve for y:

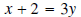
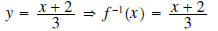[The resulting y is f^-1.]

•Verify your results by showing that

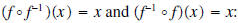
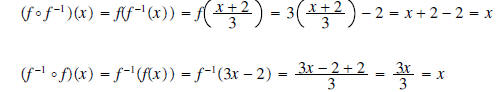
•Support graphically by showing that the graphs of f and f^-1 have symmetry about the line y=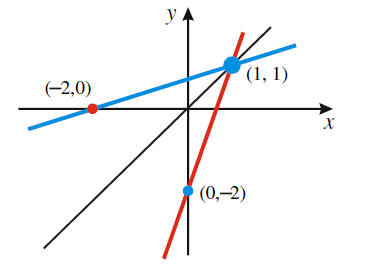x.

Example 2: The function 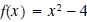is not a one-to-one function. Restrict the domain of f so that its
inverse will be a function.

Solution: Note from the graph of f, the part of the graph on either side of the line x=0 is one-to-one.
Therefore, we will restrict the domain to be

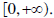
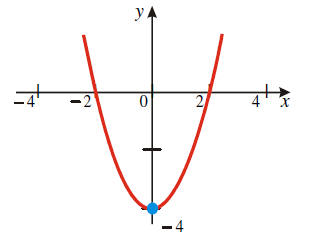
Domain of f is

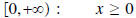
Range of f is

Example 3: In the above example we restricted the domain of 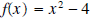so that f has an inverse
function. Find f^-1 and its domain and range.

Solution: The domain of f was restricted to x≥0, and the range is y≥-4 so that f is one-to-one.

•We write:

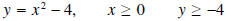
•Interchange x and y:

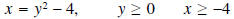[Interchange domain and range.]

•Solve for y:

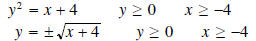
Since y≥0, we use only the positive root.

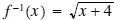
•Domain of f^-1:

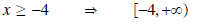
Range of f^-1: