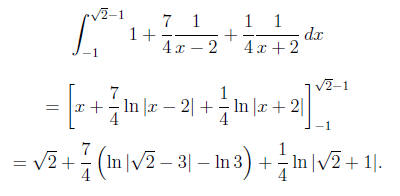Homework 6 Integration

6.2.30. We apply integration by parts letting dv = e^-x dx and u = x² so
v = -e^-x and du = 2x dx. Then,

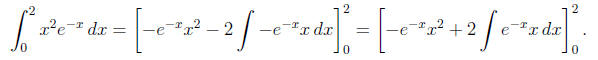
To simplify 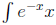dx we must apply integration by parts again with dv =
e^-x dx and u = x so v = -e^-x and du = dx. Then, we have

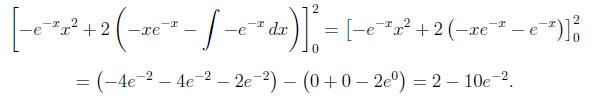
6.2.34. We apply substitution to simplify the integrand, letting u = 1+2x
so du = 2 dx and dx = 1/2 du. When x = 0, we have u = 1 + 2(0) = 1 and
when x = 1, we have u = 1+2(1) = 3. Hence, we can rewrite the integral as

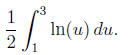
To simplify notation, we rewrite this with u = x so that we can apply inte-
gration by parts:

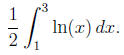
Let dv = dx and u = ln(x) so v = x and du = 1/x dx. Then we have

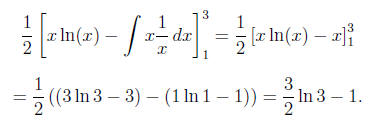
6.3.18. The integrand is a proper rational function, so we can find its
partial fraction decomposition as

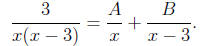
The basic equation is
3 = A(x - 3) + B(x)

which we can solve by plugging in x = 3 to get 3B = 3 so B = 1 and x = 0
to get -3A = 3 so A = -1. Hence our integral is

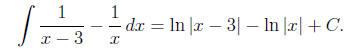
Here, we are using that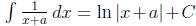 for any constant a. This can
be proved by substitution because when u = x+a, we have du = dx. Notice
that if we int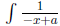egratedx then we pick up a sign, and if we integrate
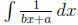then we will pick up a coefficient of 1/b .

6.3.26. The integrand is a proper rational function and the denominator
factors as x(x² - 1) = x(x - 1)(x + 1), so we can find its partial fraction
decomposition as

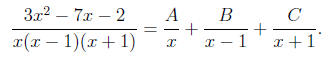
The basic equation is

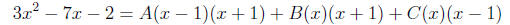
which we can solve by plugging in x = 1 to get 2B = 3 - 7 - 2 = -6 so
B = -3 and x = -1 to get 2C = 3 + 7 - 2 = 8 so C = 4 and x = 0 to get
-A = -2 so A = 2. Hence our integral is

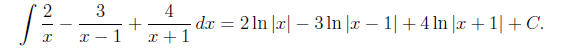
6.3.30. The integrand is not proper, so we must rst perform long division
on the rational function. We obtain

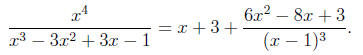
We find the partial fraction decomposition of the remainder as

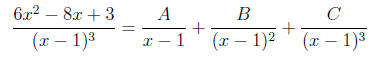
and the basic equation is

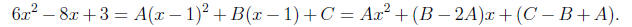
Comparing the coefficients of x² on both sides, we have A = 6. Comparing
the coefficients of x on both sides, we have B-2A = -8 so B = 4. Comparing
the coefficients of 1 on both sides, we have C -B + A = 3 so C = 1. Hence,
our integral becomes

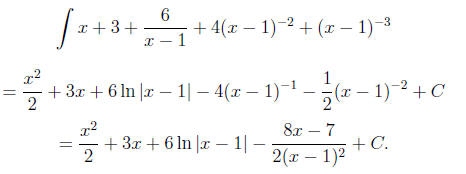
6.3.38. The integrand is not proper, so we must first perform long division
on the rational function. We obtain

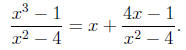
We factor the denominator of the remainder as a difference of squares x²-4 =
(x - 2)(x + 2) and find the partial fraction decomposition of the remainder
as

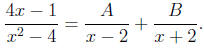
The basic equation is

and we plug in x = -2 to obtain -4B = -9 so B = 9/4 as well as x = 2 to
obtain 4A = 7 so A = 7/4 . Hence, our integral becomes

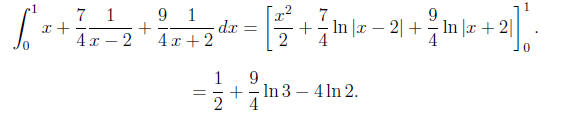
6.3.44. We begin by determining where the curve meets the x-axis by
solving 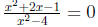for x. In order for this fraction to be zero, we must have
that the numerator is zero (and the denominator is non-zero). Hence, we
solve x² + 2x - 1 = 0 using the quadratic formula, so 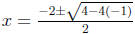The
positive root occurs at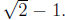(This turns out to be about 0.41.) Notice
that the denominator x² - 4 does not vanish at this root, so the function is
well-defined at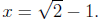

By definition, the area under this curve is

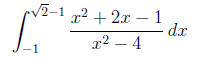
which we need partial fractions to solve. The integrand is not proper so we
must first perform long division to obtain

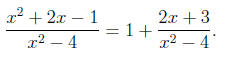
The denominator of the remainder factors as a di erence of squares (x²-4) =
(x - 2)(x + 2) and so the partial fraction decomposition is

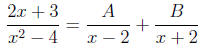
with basic equation

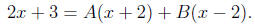
Plugging in x = -2 we get -4B = -1 so B = 1/4 and x = 2 gives 4A = 7 so
A = 7/4 . Hence, our integral becomes