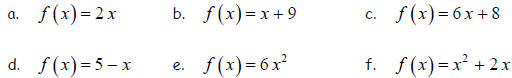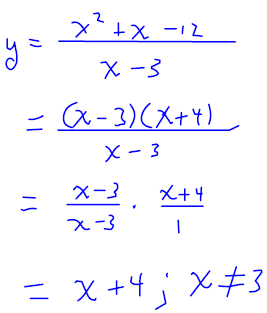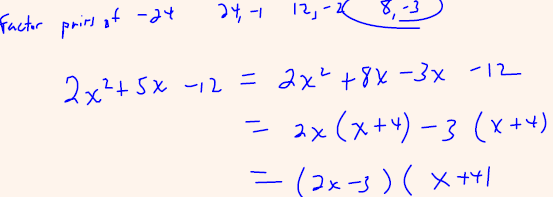Introduction to rational functions
| Textbook sections and practice problems 6.1: 1 – 10 all, 13, 15, 25-59 odd, 93, 97, 95 |
| Definition A function f whose formula can be written in the form 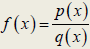 where p and q are where p and q areboth polynomial functions is called a rational function. |
Example 1
Graph the function 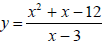 on your calculator and
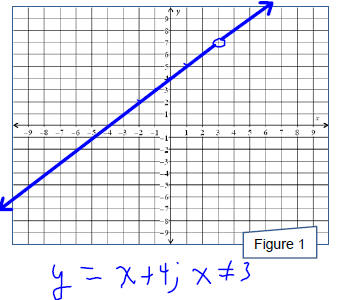
carefully copy the graph onto Figure 1.
on your calculator and
carefully copy the graph onto Figure 1.
State the domain of the function. Finally, write the equation for the function
in simplified form.
|
 |
Example 2
Graph the function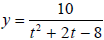 on your calculator and
carefully copy the graph onto Figure 2.
on your calculator and
carefully copy the graph onto Figure 2.
State the domain of the function. Finally, write the equation for the function
in simplified form.
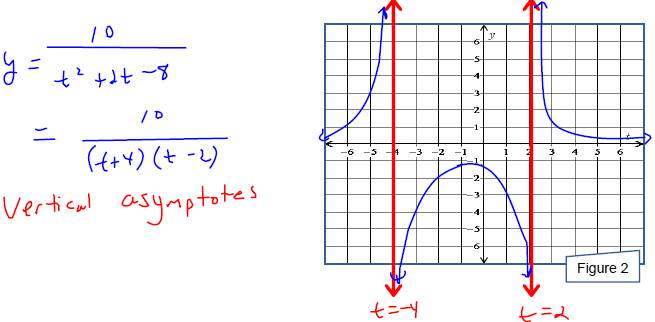
Recall To factor t2 + 2t − 8 we first need to find an integer factor pair of −8 that adds to 2 . |
Example 3
Simplify the formula for 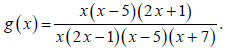 Make sure that you
state any
Make sure that you
state any
necessary domain restrictions. State any other numbers that are not in the
domain of g .
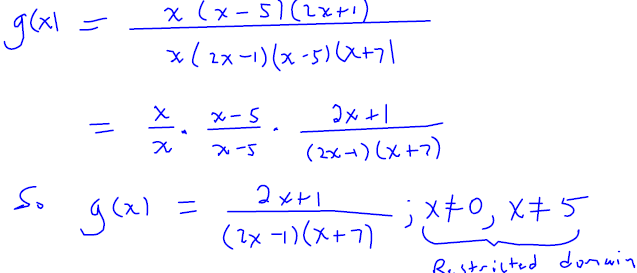
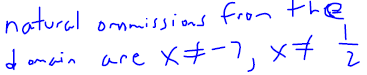
Example 4
Simplify 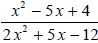 . Make sure that you state any
necessary domain restrictions.
. Make sure that you state any
necessary domain restrictions.
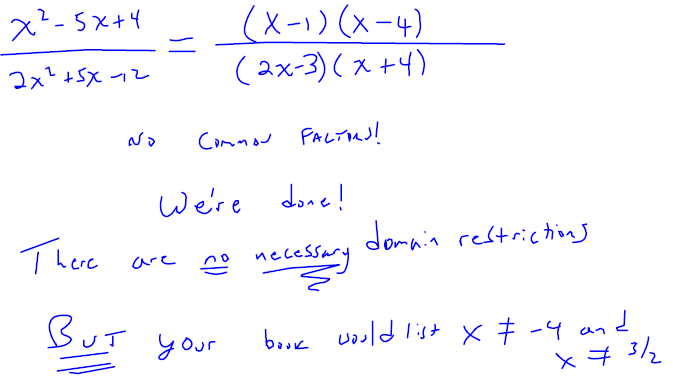
Recall
To factor 2 x2 + 5 x −12 we first need to find an integer factor pair of (2)(−12) that adds to 5
|
Example 4
Simplify each rational expression; make sure that you state any necessary
restrictions to the
domains.
Simplify 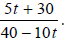
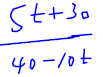
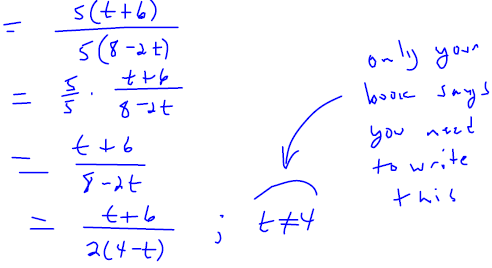
Simplify 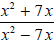
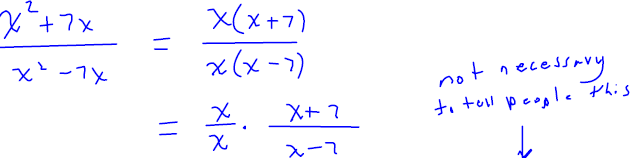
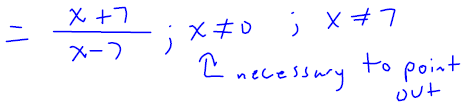
Simplify 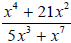
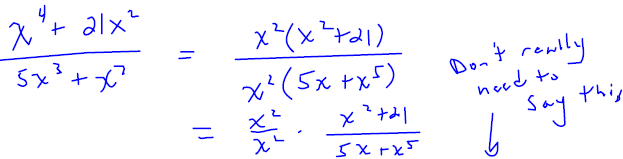 |
||
 |
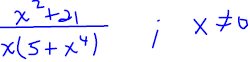 |
|
Example 5
Simplify 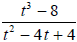 . State any necessary restrictions
on the domain.
. State any necessary restrictions
on the domain.
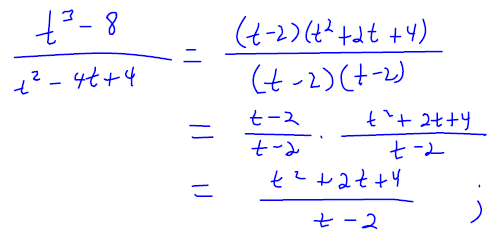

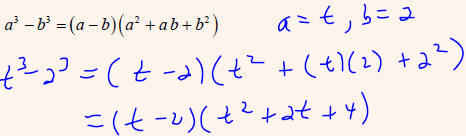 |
Example 6
Simplify the formula for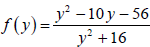 . What is the domain
of f ?
. What is the domain
of f ?
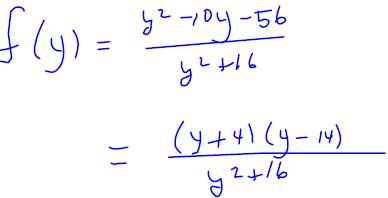 |
 |
Thinking about what y couldn't be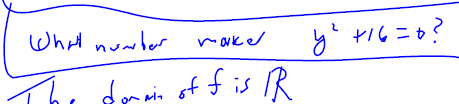 |
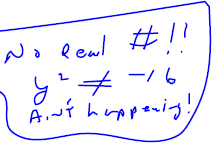 |
|
a2-b2=(a-b) (a+b) a2+b2 is psime! |
|
Example 7
Simplify the formula for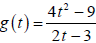 . State any necessary
restrictions on the domain. What
. State any necessary
restrictions on the domain. What
other numbers are not in the domain of g ?
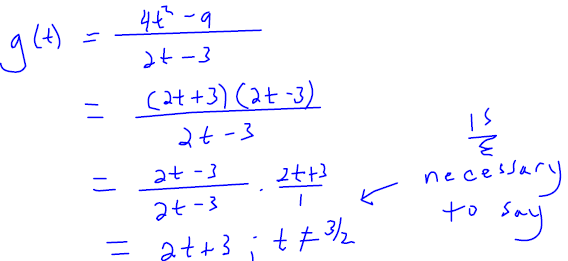
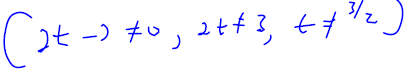
Example 8
Simplify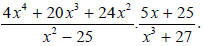
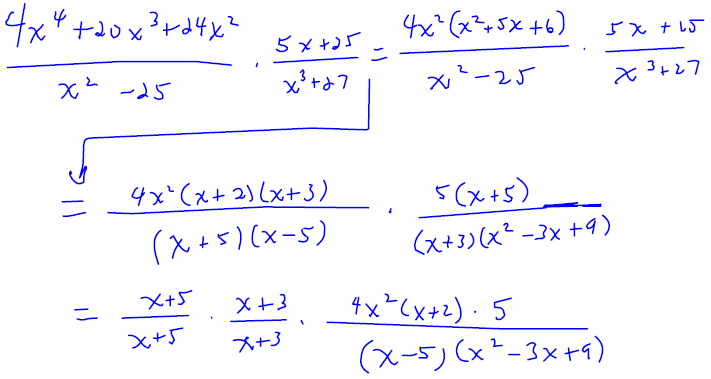 |
||
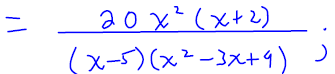 |
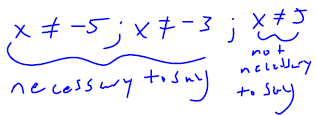 |
|
Example 9
Suppose that f (x) = 3 x + 2 , g (t ) = 2 − 7t , and m(x) = x2
a. Find and simplify f (x + h) , g (t + h) , and m(x + h) .
b. Find and simplify 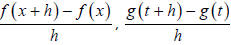 , and
, and
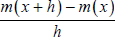
Additional practice problems for you
1. Complete simplify each expression. Make sure that you state all necessary
domain restrictions.
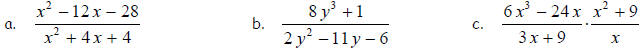
2. Simplify each function formula making sure that you
state any necessary domain restrictions.
Then state the domain of the function using interval notation.

3. Find and completely simplify f (x + h) for each of the following function.
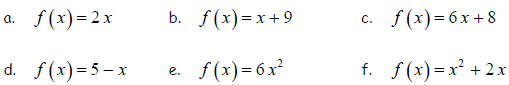
4. Find and completely simplify
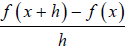 for each of the following function.
for each of the following function.