Sample Test Problems for Mathematics
1. Write two story problems for 27 ÷ 4, one for each of
the two interpretations of division.
2. For each of the following story problems, write a division problem that
solves the problem,
give an appropriate answer to the problem, and say which of the two
interpretations of division
is used (the “how many groups?” or the “how many in each group?” interpretation,
with or
without remainder).
(a) If a box of laundry detergent costs $5 and washes 38 loads of laundry, then
how much
does the detergent for one load of laundry cost?
| division problem | appropriate answer | which interpretation of division? |
(b) If a box of laundry detergent costs $5 and washes 38 loads of laundry, then
how many
loads of laundry can you wash for $1?
| division problem | appropriate answer | which interpretation of division? |
(c) If a box of laundry detergent costs $5 and washes 38 loads of laundry, and
if you wash 6
loads of laundry per week, then how many weeks will a box of laundry detergent
last?
| division problem | appropriate answer | which interpretation of division? |
3. For each of the following story problems, write the corresponding division
problem, state which
interpretation of division is involved (the “how many groups?” or the “how many
in each
group?”, with or without remainder), and solve the problem.
(a) Given that 1 quart is 4 cups, how many quarts of water is 35 cups of water?
(b) If your car used 15 gallons of gasoline to drive 330 miles, then how many
miles per gallon
did your car get?
(c) If you drove 240 miles at a constant speed and if it took you
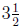hours, then how fast were
you going?
(d) Given that 1 inch is 2.54 centimeters, how tall in inches is a woman who is
153 cm tall?
(e) Will needs to cut a piece of wood 0.67 of an inch thick, or just a little
less thick. Will’s
ruler shows sixteenths of an inch. How many sixteenths of an inch thick should
Will cut
his piece of wood?
4. What day of the week will it be 100 days from today? Use mathematics to solve
this problem.
Explain your solution.
5. If January 1, 2003 is on a Wednesday, then what day of
the week will January 1, 2004 fall on?
Use mathematics to solve this problem. Explain your solution.
6. What is 1 billion seconds in terms of years, days, hours, and minutes?
Explain why you can
solve this problem the way you do.
7. Make up and solve three different story problems for 9 ÷ 4.
(a) In the first story problem, the answer should best be expressed as 2,
remainder 1.
(b) In the second story problem, the answer should best be expressed as
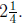
(c) In the third story problem, the answer should best be expressed as 2.25.
8. (a) Is 0 ÷ 10 defined or not? Write a story problem for 0 ÷ 10 and use the
story problem to
discuss whether or not 0 ÷ 10 is defined.
(b) Is 10 ÷ 0 defined or not? Write a story problem for 10 ÷ 0 and use the story
problem to
discuss whether or not 10 ÷ 0 is defined.
9. (a) Explain why 12÷ 0 is not defined by rewriting the problem 12÷ 0 =? as a
multiplication
problem.
(b) Explain why 12 ÷ 0 is not defined by writing a story problem for 12 ÷ 0.
10. Is 5 ÷ 0 defined? Is 0 ÷ 5 defined? Explain your answers clearly.
11. Taylor is working on the following problem: There are 450 stickers to be put
in packages of 16.
How many packages of stickers can we make, and how many stickers will be left
over? Here are
Taylor’s ideas:
Ten packages will use up 160 stickers. After another 10 packages, 320 stickers
will
be used up. After 1 more package, 336 stickers are used. Then there are only 14
stickers left and that’s not enough for another package. So the answer is 21
packages
of stickers with 14 stickers left over.
Explain why the equations
10 · 16 + 10 · 16 + 1 · 16 + 14 = 450
(10 + 10 + 1) · 16 + 14 = 450
21 · 16 + 14 = 450
correspond to Taylor’s work and explain why the last equation shows that 450 ÷
16 = 21,
remainder 14.
12. Amanda is working on the division problem 358 ÷ 25. Amanda’s work appears in
Figure 1
(a) Explain why Amanda’s strategy makes sense. It may help you to work with a
story
problem for 358 ÷ 25.
(b) Write equations that correspond to Amanda’s work and that demonstrate that
358÷25 =
14, remainder 8.
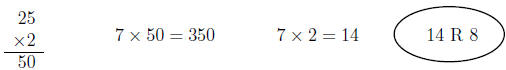
Figure 1: Amanda’s work for 358 ÷ 25
13. Arthur is working on the division problem 358 ÷ 25. Arthur writes:
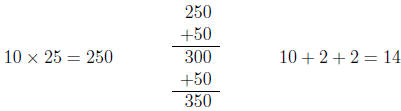remainder 8
(a) Explain why Arthur’s strategy makes sense. It may help
you to work with a story problem
for 358 ÷ 25.
(b) Write equations that correspond to Arthur’s work and that demonstrate that
358÷25 = 14,
remainder 8.
14. Zoe is working on the division problem 358 ÷ 25. Zoe writes:
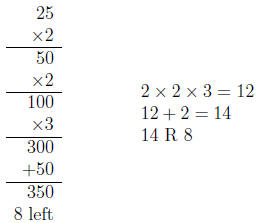
(a) Explain why Zoe’s strategy makes sense. It may help
you to work with a story problem
for 358 ÷ 25.
(b) Write equations that correspond to Zoe’s work and that demonstrate that
358÷25 = 14,
remainder 8.
15. Assume that you don’t know any kind of longhand method of division. Explain
how you can
use reasoning to calculate 495 ÷ 35. It may help you to work with a story
problem.
16. (a) Write two story problems for 1957 ÷ 6, one for the “how many in each
group?” interpre-
tation and one for the “how many groups?” interpretation.
(b) Assume that you don’t know any longhand method of division. Explain how you
can use
reasoning to calculate 1957÷6. Use one of your story problems from part (a) to
interpret
your steps.
17. (a) Write a story problem for 3458 ÷ 6 using the “how
many groups?” interpretation of
division.
(b) Use the scaffold method to calculate 3458÷ 6. Interpret each step in the
scaffold method
in terms of your story problem.
18. (a) Use standard long division to calculate 2639 ÷ 3.
(b) Interpret each step in your calculation in part (a) in terms of the
following problem. You
have 2639 toothpicks bundled into 2 thousands, 6 hundreds, 3 tens, and 9
individual
toothpicks. If you divide these toothpicks equally among 3 groups, how many
toothpicks
will each group get and how many toothpicks will be left over?
19. Allie calculates 8798 ÷ 14 as follows.
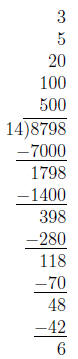
Describe how Allie could have solved the division problem
using fewer steps. Even though Allie
used more steps than necessary, is her work still mathematically valid? That is,
does Allie’s
work correspond to legitimate reasoning? Explain.
20. A student calculates 89, 998 ÷ 9 as follows, and concludes that 89, 998 ÷ 9
= 10, 000 − 1,
remainder 7, which is 9999, remainder 7.
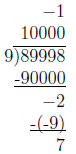
Even though it is not conventional to use negative numbers
in a scaffold, explain why the
student’s method does correspond to legitimate reasoning. Write a simple story
problem for
89, 998÷9 and use your story problem to discuss the reasoning that corresponds
to the scaffold.
21. Use the meaning of fractions and the meaning of division to explain why
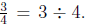Your
explanation should be general, in the sense that you could see why the equation
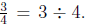
would still be true if other numbers were to replace 3 and 4.
22. Describe how to get the mixed number answer to 19÷6 from the whole number
with remainder
answer. By considering a simple story problem, explain why the method you
describe makes
sense.
23. Describe how to use division to write the improper fraction
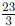as a mixed number and explain
why the procedure you describe makes sense.
24. (a) Use long division to determine the decimal number answer to 953 ÷ 6 to
the hundredths
place.
(b) Interpret each step in your long division calculation in part (a) in terms
of dividing $953
equally among 6 people.
25. Use the large, subdivided square in Figure 2 to help you explain why the
decimal representation
of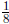 
is 0.125.
Figure 2: Show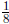
26. Describe how to use dimes and pennies to help you explain why
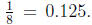Explain your
reasoning.
27. (a) Use long division to determine the decimal representation of
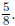
(b) Interpret the steps to the hundredths place in your long division in part
(a) in terms of
dividing $5 equally among 8 people.
28. Plot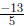 
and at least
two other nearby integers on a number line and explain why you have
plotted these numbers appropriately.
29. Wu has been making errors on his division problems. Here are some of Wu’s
answers:
150 ÷ 7 = 21.3
372 ÷ 8 = 46.4
154 ÷ 12 = 12.10
What is Wu likely to be confused about? Explain.