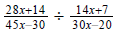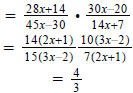Simplification, Multiplication and Division of Rational
Expressions
A rational expression is a fraction where both the
numerator and denominator are
polynomials.
Example: 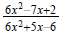 is a rational expression.
Part 1: Simplifying Rational Expressions
Like number fractions, a rational expression can
be simplified by canceling common
factors from the numerator and the denominator. |
Question 29: Simplify
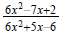
Factor the numerator and the denominator.
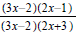
Cancel the common factor 3x−2
So the simplified rational expression is: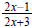
Can we cancel the 2x 's? NO!!!!! Because it is not a
factor of either the numerator or the
denominator.
Question 16 Now you do this one: Simplify
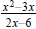
Factor: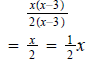 
Either answer is correct.
Part 2: Multiplying Rational Expressions
You multiply rational expressions just like you
do fractions. You make life easy on
yourself if you cancel factors that are the same in the numerator and
the denominator
before you multiply things out. [Don't say I didn't warn you!!!] |
Remember you must always simplify your answer!
Question 32:
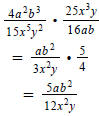
Question 47:
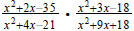
[Resist the temptation to cancel the 18's or the x2 's.
Why?]
Factor, factor, factor.
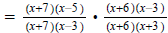
We can cancel the x+7, the x+6 and the x-3
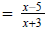
Question 36 Now you multiply this one:
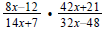
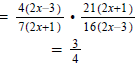
Part 3: Division of Rational Expressions
Again we treat rational expressions like we did
fractions. When we divide fractions we
invert (flip) the second expression and multiply. |
|
Question 64: Divide |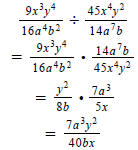
 |
|
Flip the second fraction: |
|
Now cancel like terms: |
| |
Question 77: Divide
|
 |
|
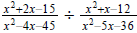Flip the second fraction: |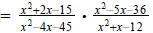
 |
|
Now factor everything: |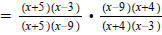
 |
|
And cancel: |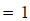
 |
Notice that when everything cancels, this means the
numbers in the denominator divide
into those in the numerator exactly once.
Question 66 Now you divide this one:
|