Polynomial Division;The Remainder and Factor Theorems

I. Polynomial Division

When we divide one polynomial by another, we obtain a quotient and a remainder. If the
remainder is 0, then the divisor is a factor of the dividend.

For example, when we divide x^3 + 6x^2 – 25x + 18 by x + 9, we get x^2 – 3x + 2 with nothing
remaining. In this case, x^3 + 6x^2 – 25x + 18 is called the dividend, x + 9 is the divisor,
x^2 – 3x + 2 is the quotient, and 0 is the remainder.

To check our division, we can multiply the divisor, d(x), times the quotient, Q(x), and add the
remainder, R(x). This should yield the dividend, P(x). This is called the division algorithm.
d(x) · Q(x) + R(x) = P(x) divisor · quotient + remainder = dividend

A. Long Division
To divide one polynomial by another using long division, we use four repeated steps:
1. Divide
2. Multiply
3. Subtract (or add the opposite)
4. Bring down

Example 1
Use long division to determine if x + 5 is a factor of h(x) = x^3 – x^2 – 17x – 15. (#2 p. 287)

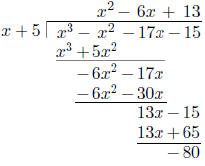
Since the remainder is not 0, x + 5 is not a factor of h(x).

Example 2
Given the polynomial P(x) = 2x^3 – 3x^2 + x – 1 and the divisor d(x) = x – 3, (#6 p. 287)
use long division to find the quotient Q(x) and the remainder R(x) when
P(x) is divided by R(x). Then express P(x) in the form d(x) · Q(x) + R(x).


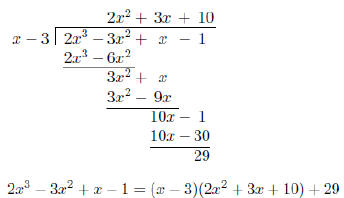
B. Synthetic Division

Synthetic Division is a “collapsed” version of polynomial division. We can use it
to divide a polynomial function f(x) by a divisor of the form x – c. If the divisor is x – 5,
c = 5. If the divisor is x + 3, c = –3.The steps of synthetic division are as follows.

1. Write c in a backwards L and then write down the coefficients of the dividend.
If any term of the dividend is missing, you must insert 0 as a placeholder for that
position.

2. Leave some space below the coefficients and then draw a horizontal bar. Rewrite the
first coefficient below the horizontal bar.

3. Multiply c by the number under the bar and record the result in the next column.

4. Add.

5. Repeat steps 3 and 4 as necessary.

6. Circle the last number under the bar. This is your remainder.

7. The other numbers under the bar are the coefficients of the quotient. The quotient is
always one degree less than the dividend.

Example 3
Use synthetic division to find the quotient and the remainder when x^3 – 3x + 10 (#14 p. 287)
is divided by x – 2.

c = 2 and the coefficients of the dividend are 1 0 –3 10. We must insert a placeholder in
the second column because the x^2 term is missing.

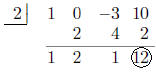
Q(x) = x^2 + 2x + 1
R(x) = 12

II. The Remainder Theorem
If a number c is substituted for x in the polynomial f(x), then the result f(c) is the remainder
that would be obtained by dividing f(x) by x – c. That is,
if f(x) = (x – c) ·Q(x) + R(x), then f(c) = R.

Example 4
Given f(x) = x^3 + 7x^2 – 12x – 3, use synthetic division to find the function #24 p. 287
value f(–2).
c = –2 and the coefficients of the dividend are 1 7 –12 –3.

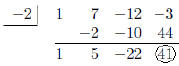
f(–2) = 41

III. The Factor Theorem
For a polynomial f(x), if f(c) = 0, then x – c is a factor of f(x).

Example 5
Use synthetic division to determine whether –4 and 2 are zeros of the polynomial #32 p. 288
function f(x) = 3x^3 + 11x^2 – 2x + 8.

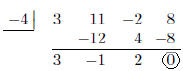
f(–4) = 0, so –4 is a zero of f(x) and x + 4 is a factor of f(x).

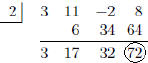
f(2) ≠ 0, so 2 is not a zero of f(x) and x – 2 is not a factor of f(x).

Example 6
Factor the polynomial f(x). Then solve the equation f(x) = 0. #42 p. 288
f(x) = x^3 +2x^3 – 13x + 10
Hint: Factor the constant and then check to see if its factors are zeros of f(x).
a0 = 10 the factors of 10 are: 1, –10, –1, 10, 2, –5, –2, 5
Let’s start by checking 1.

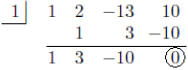
Since 1 produced a remainder of 0, we know x – 1 is a factor of f(x) and 1 is a zero.
We can find the other two zeros and factors by setting the quadratic quotient equal to 0 and
solving for x.
x^2 + 3x – 10 = 0 → (x + 5) (x – 2) = 0 → x = –5 and x = 2
Therefore f(x) = (x – 1)(x + 5)(x – 2) and the solutions of the equation f(x) = 0 are 1, –5, and 2.

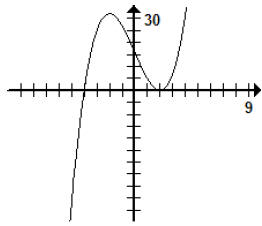
Example 7
Use synthetic division and the remainder theorem to find the zeros of #52 p. 288
f(x) = x^3 – 12x + 16 and then use the procedure from section 3.2 to graph the
function.
The leading term of the polynomial is x^3. Since n is odd and the leading coefficient is
positive, the left hand is down, and the right hand is up. The maximum possible number of
x-intercepts is 3 and the maximum number of turns is 2.
a0 = 16 the factors of 16 are 1, –16, –1, 16, 2, –8, –2, 8, 4, –4

Let’s start by checking 1.

Since the remainder ≠ 0, 1 is not a zero of f(x). Let’s try 2.

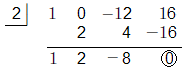
Since the remainder = 0, 2 is a zero of f(x).
We can find the other two zeros and factors by setting the quadratic quotient equal to 0 and
solving for x.
x^2 + 2x – 8 = 0 → (x – 2) (x + 4) = 0 → x = 2 and x = –4
–4 occurs with a multiplicity of 1, so the graph crosses the x-axis at x = –4
2 occurs with a multiplicity of 2, so the graph is tangent to the x-axis at x = 2
 

Interval	x	y
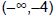	–5	–49
(–4, 2)	0	16
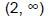	3	7

y-intercept: (0, 16)
additional points
 

x	y
-5	-49
-4	0
-3	25
-2	32
-1	27
0	16
1	5
2	0
3	7

Graph