ITERATIVE METHODS FOR SOLVING LINEAR EQUATIONS
Gauss-Seidel Iterative Method
The Gauss-Seidel iterative method of solving for a set of
linear equations can be thought
of as just an extension of the Jacobi method. Start out using an initial value
of zero for
each of the parameters. Then, solve for x1 as in the Jacobi method. When solving
for x2,
insert the just computed value for x1. In other words, for each calculation, the
most
current estimate of the parameter value is used. To see how the Gauss-Seidel
method
works, lets use the values in the last example. The initial estimates are set to
zero. Then,
the results from the first iteration are shown as:
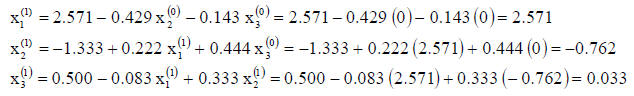
The next iteration is performed in a similar fashion. It can be shown as:
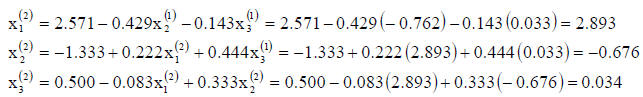
A Fortran program was written to solve this problem. The results are shown in
the next
table.
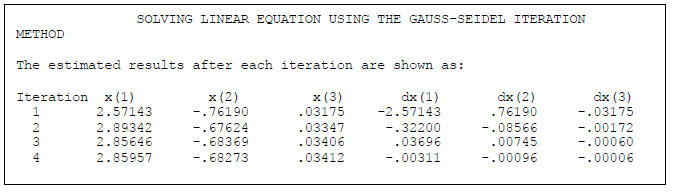
As with the Jacobi method, the results from the Gauss-Seidel method are
essentially
correct. The Fortran program used to compute the Jacobi iteration method was
modified
to solve for the Gauss-Seidel iterative method. The program is shown as follows:
c Program to solve a linear equation using the Gauss-Seidel
c Iteration method
c
IMPLICIT none
REAL*8 coef(3,4), d, dx(3), x(3,4), xn(3), xnp(3)
INTEGER i, iter, iterate,j, no, nv
DATA iterate /0/
c
c The data are entered into the program using a data file called
c gauss.dat. It has the following row values
c number of equations
c number of variables
c x(1) x(2) x(3) solution for the first equation
c x(1) x(2) x(3) solution for the second equation
c x(1) x(2) x(3) solution for the third equation
c
OPEN (4, file = 'gauss.dat')
OPEN (6, file = 'results')
c
c no is the number of equations and nv is the number of variables
c
read(4,*) no
do 5 i=1,no
xn(i) = 0.d0
xnp(i) = 0.d0
5 continue
read(4,*) nv
write(6,901)
c
c The coefficients for the variables are read in the matrix x with
c the solution to the equations being the last column
c
do 10 i=1,no
read(4,*)(x(i,j),j=1,no+1)
c
c d is the coefficient for the variable that is being solved for
c it forms the denominator to compute the real number for the
c remaining coefficients
c
d = x(i,i)
do 7 j=1,no+1
coef(i,j) = x(i,j)/d
7 end do
c
c Because the Jacobi method solves for the unknown variable with
c respect to the current estimates of the other variables, the
c coefficient for the variable is made to be zero for subsequent
c use in the loop to compute the adjusted estimates
c
coef(i,i) = 0.d0
write(6,900)(x(i,j),j=1,nv+1)
10 end do
write(6,902)
do 13 i=1,no
write(6,900)(coef(i,j),j=1,nv+1)
13 end do
write(6,903)
15 iter = 0
c
c iterate is just a counter to keep track of the number of iterations
c
iterate = iterate+1
c
c Solve for the estimate of the unknown parameters
c
do 20 i=1,no
xn(i) = coef(i,nv+1)
do 18 j=1,nv
Iterative Methods for Solving Linear Equations Page 7
xn(i) = xn(i) - coef(i,j)*xn(j)
18 end do
20 end do
c
c dx is a vector showing the change in the estimate of the variable
c with respect to the estimated value used in the previous iteration
c
do 50 i=1,no
dx(i) = xnp(i) - xn(i)
xnp(i) = xn(i)
c
c Test to see if the change is greater than the threshold
c If it is, then the variable iter is made equal to 1
c At the beginning of each loop, this value is made equal to 0
c If iter is 1 then this means to iterate again
c
if (dabs(dx(i)).gt.0.01d0) iter = 1
c
c Update the estimated parameter value
c
xn(i) = xnp(i)
50 continue
write(6,904)iterate,(xn(i),i=1,nv),(dx(i),i=1,nv)
if (iter.gt.0) go to 15
900 FORMAT(5x,4(f10.4,5x))
901 FORMAT(15x,'SOLVING LINEAR EQUATION USING THE GAUSS-SEIDEL ITERATI
1ON METHOD',//,'The coefficients to the equations with the solution
1 at the end are:',/)
902 FORMAT(//,'Rearranging the equations to solve for the unknown vari
1ables yields',/,5x,'the following coefficients: ',/)
903 FORMAT(//,'The estimated results after each iteration are shown as
1:'//,'Iteration',2x,'x(1)',9x,'x(2)',9x,'x(3)',7x,'dx(1)',7x,'dx(2
2)',7x,'dx(3)')
904 FORMAT(i3,4x,6(f10.5,2x))
stop
en
A more sophisticated subroutine for solving the
Gauss-Seidel is shown as [source
unknown]:
c-----------------------------------------------------------------------
c
c Gauss-Seidel Iterative Method
c *****************************
c
c This subroutine obtaines the solution to n linear equations by Gaussc
Seidel iteration. An initial approximation is sent to the subroutine
c in the vector x. The solution, as approximated by the subroutine is
c returned in x. The iterations are continued until the maximum change
c in any x component is less than tol. If this cannot be accomplished
c in niter iterations, a non-zero error flag is returned. The matrix
c is to be arranged so as to have the largest values on the diagonal.
c (from "Applied Numerical Analysis," C.F. Gerald, p 138)
ccc c INPUT/OUTPUT VARIABLES:
c
c a(n,n) coefficient matrix with largest values on diagonal
c b(n) right hand side vector
c x(n) solution vector (initial guess)
c n Dimension of the system you're solving
c ndim Dimension of matrix a (Note: In the main program,
c matrix a may have been dimensioned larger than
c necessary, i.e. n, the size of the system you're
c decomposing, may be smaller than ndim.)
c niter Number of iterations
c tol tolerance for solution
c ierr Error code: ierr=0 - no errors; ierr=1 - the
c solution was not obtained in maximum iterations
c c-----------------------------------------------------------------------
dimension a(ndim,ndim),b(ndim),x(ndim)
ierr = 0
c
c We can save some divisions by making all the diagonal
c elements equal to unity:
c
do 1 i=1,n
temp = 1.0 / a(i,i)
b(i) = b(i) * temp
do 2 j=1,n
a(i,j) = a(i,j) * temp
2 continue
1 continue
c
c Now we perform the iterations. Store max change in x values for
c testing against tol. Outer loop limits iterations to niter:
c
do 3 iter=1,niter
xmax = 0.0
do 4 i=1,n
temp = x(i)
x(i) = b(i)
do 5 j=1,n
if(i.ne.j) then
x(i) = x(i) - a(i,j)*x(j)
endif
5 continue
if(abs(x(i)-temp).gt.xmax) xmax = abs(x(i)-temp)
4 continue
if(xmax.le.tol) return
3 continue
c
c Normal exit from the loop means non-convergent solution. Flag the
c error and pass control back to the calling routine:
c
ierr = 1
return
end
These iterative methods can also be very effectively
programmed in a spreadsheet like
Excel. For example, the Jacobi method of solving for linear equations can be
shown as:
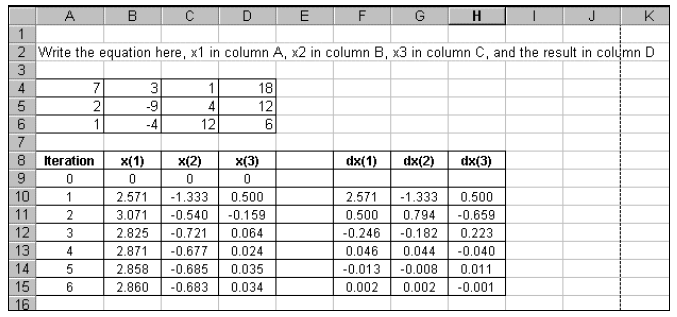
The formulas for computing x1 and x2 within the
spreadsheet are shown as:
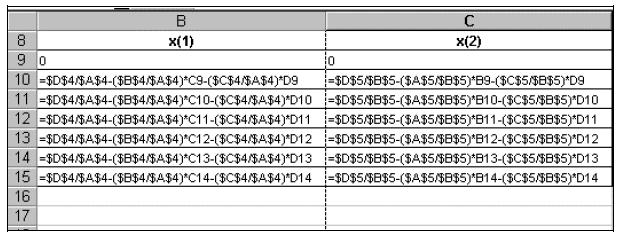
It is a simple process of copying and pasting to add more lines to solve the
equations. In
a similar fashion, the Gauss-Seidel method can also be programmed within Excel
to
arrive at the same results, as shown in the following figure.
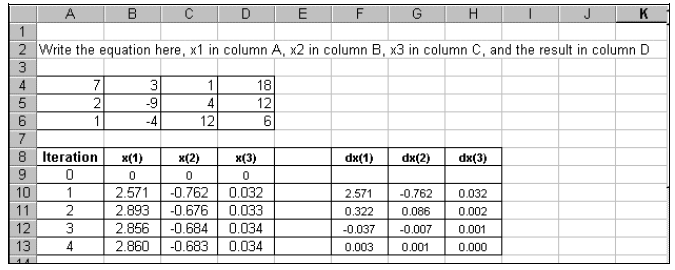
While the Gauss-Seidel method appears to be the best in this example, this is
not always
the case. In fact, it is very possible that the solution from either of these
methods could
be in error. For example, lets look at the following equations:
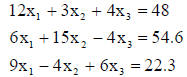
Then, using a criteria of 0.1 (this is the significant figures for the input
values) to stop the
iterations, the solution using the Jacobi method can be shown to be:
SOLVING LINEAR EQUATION USING THE JACOBI ITERATION METHOD
The estimated results after each iteration are shown as:
| Iteration | x(1) | x(2) | x(3) | dx(1) | dx(2) | dx(3) |
| 1 | 4.00000 | 3.64000 | 3.71667 | 4.00000 | 3.64000 | 3.71667 |
| 2 | 1.85111 | 3.03111 | .14333 | -2.14889 | -.60889 | -3.57333 |
| • | ||||||
| 13 | 2.65235 | 3.05960 | 1.84979 | .04225 | -.01281 | .11114 |
| 14 | 2.61850 | 3.07234 | 1.77788 | -.03384 | .01274 | -.07191 |
The same results using the Gauss-Seidel method, same criteria, are:
SOLVING LINEAR EQUATION USING THE GAUSS-SEIDEL ITERATION
METHOD
The estimated results after each iteration are shown as:
| Iteration | x(1) | x(2) | x(3) | dx(1) | dx(2) | dx(3) |
| 1 | 4.00000 | 2.04000 | -.92333 | -4.00000 | -2.04000 | .92333 |
| 2 | 3.79778 | 1.87467 | -.73022 | .20222 | .16533 | -.19311 |
| 3 | 3.77474 | 1.93538 | -.65519 | .02304 | -.06071 | -.07503 |
These are markedly different results.


