Evaluating Variable Expressions
2.1.1 Evaluating Variable Expressions
Variable, Term and Coefficient
A variable is a letter used to represent a quantity
that is unknown,
or a quantity that can change or vary.
e.g.
x = the price of one share of Microsoft stock
y = the cost of a new car
h = a student’s height
m = miles per gallon of an automobile
The terms of a variable expression are the addends of the expression. Consider
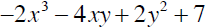
a. Rewrite the expression using only addends.
b. List the variable terms
c. List the constant term.
d. What are factors?
e. How many factors are in the first term? List them.
f. How many factors are in the second term? List them
The numerical coefficients of an expression, or
simply the
coefficients, are the numerical factors of the variable terms.
g. List the coefficients in
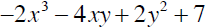
Evaluate an Expression
To evaluate a variable expression means to replace
the variables
with numbers and perform all indicated operations (addition,
subtraction, multiplication, division, etc); the result will be a single
number.
Rule on Substituting Negative Numbers into Variables
Whenever a negative number is substituted into a variable,
the
negative number must be placed inside a set of parentheses.
Furthermore, if a negative number is raised to an exponent, the
negative number must be inside a set of parentheses and the
exponent must be outside the parentheses.
Example 1 Evaluate x^2 when
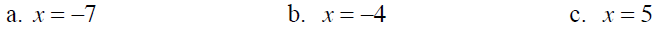
Example 2 Evaluate −b^2 when
Example 3 Evaluate −y^2 − 3xy when

Example 4 Evaluate
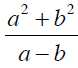
when

Example 5 Evaluate
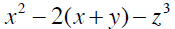 when
when

Example 6 Evaluate
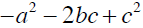

2.2.1 Properties of Real Numbers
If a, b, and c are real numbers, then
| Operation | ||
| Property | Addition | Multiplication |
| Commutative
means order does |
Commutative property of addition |
Commutative property of multiplication |
| Associative means grouping does not matter |
Associative property of addition |
Associative property of multiplication |
| Inverse The additive inverse is the opposite. The multiplicative inverse is the reciprocal. |
Inverse property of addition |
Inverse property of multiplication |
| Zero | Addition property of zero |
Multiplication property of zero |
| One | Multiplication property of one |
|
The Distributive Property
For any real numbers a, b, and c
a(b + c) = ab + ac and (b + c)a = ab + ac
Example 1
Rewrite each expression using the distributive
property. Then evaluate the expression.

solution
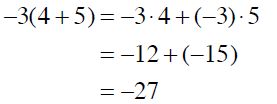
Example 2 Identify the property that justifies each statement
a. 12 + (−12) = 0
b. (3+11)+15 = 3+ (11+15)
c. (4 * 7) *5 = (7 * 4) *5
d. Any number times its reciprocal equals one.
e. Any number times zero is zero.
f. The sum of any number and its additive inverse is zero.
g. The order in which two numbers are multiplied does not matter.
Example 3 Create an example that shows division
does not
have the commutative property.
Example 4 Create an example that shows subtraction
does not
have the associative property.
2.2.2 Combining Like Terms
Terms are addends. Like Terms of an
expression are terms that
have identical variable parts. Constant terms are always like terms.
To combine like terms means to add the coefficients of like terms,
keeping the variable part the same. This is possible because of the
distributive property. For example,
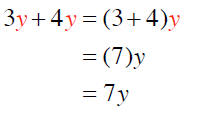
Example 5 Use the distributive property to simplify each expression.

Example 6 Simplify each expression
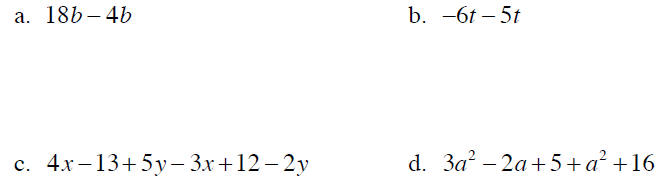
2.2.3 Use the Properties of Multiplication to Simplify
Variable Expressions
Example 7 Use the Commutative and Associative
Properties of
Multiplication to simplify each expression.
a. −4(c * 7)
| −4(c * 7) = −4(7c) | Commutative property of multiplication |
| = (−4 * 7)c | Associative property of multiplication |
| = −28c |

Example 8 Simplify each expression
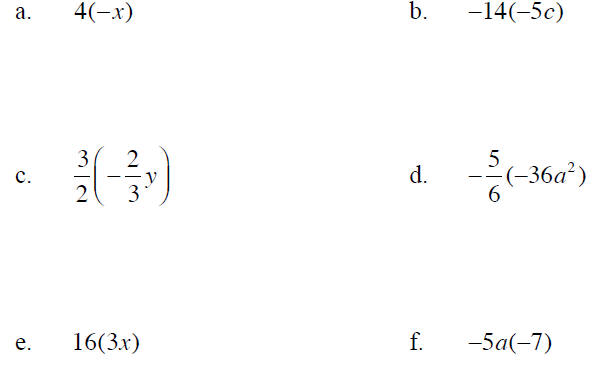
2.2.4 Simplify Variable Expressions using the
Distributive Property
Example 9 Simplify each expression.
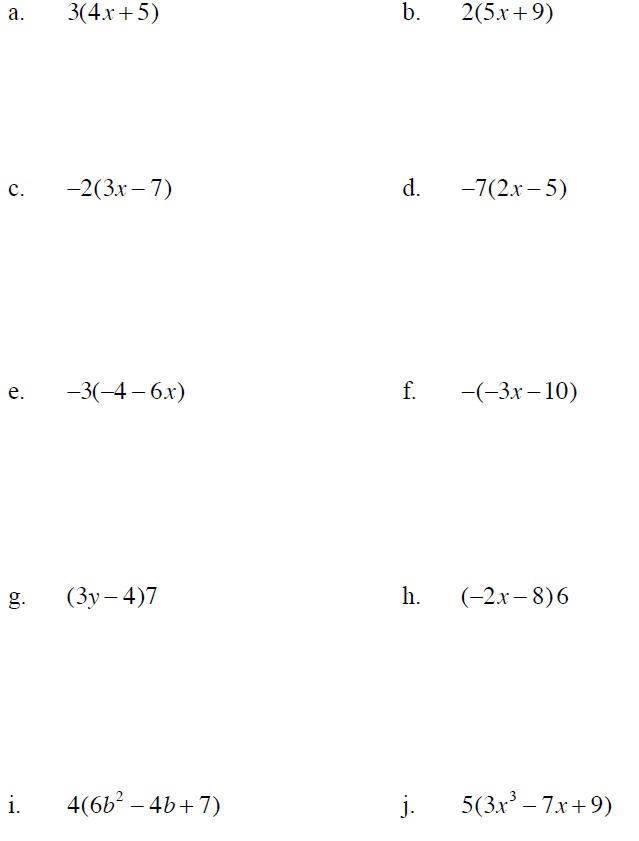
2.2.5 Simplify General Expressions
Steps to Simplify General Expressions
1. Use the Distributive Property to remove any grouping
symbols starting from the innermost set and working outward.
2. Combine like terms.
3. Write the terms in alphabetical order with the constant term last.
Example 10 Simplify each expression
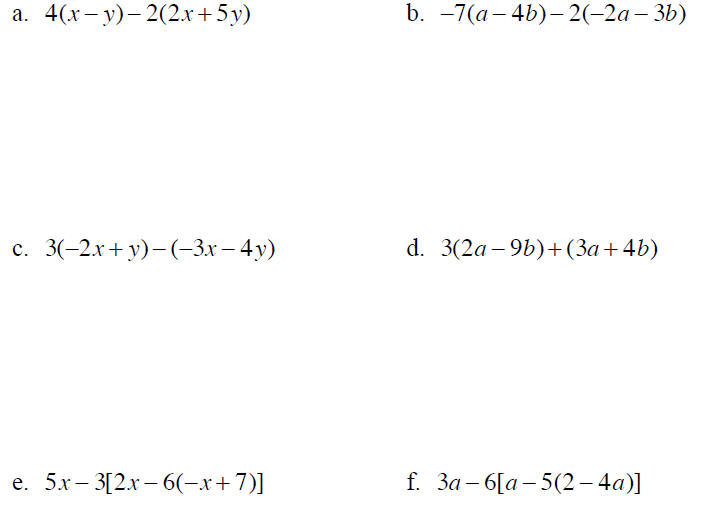
2.3 Translating Verbal Expressions into Variable
Expressions
In the expressions below marked with an asterisk (*),
the actual
operation (+, −, ×, ÷ ) occurs at the word “and” in the sentence.
| Verbal Expression | Variable Expression | |
| Addition Phrases |
6 added to y | y + 6 |
| 8 more than x | x + 8 | |
| *the sum of x and z | x + z | |
| t increased by 9 | t + 9 | |
| *the total of 5 and y | 5 + y | |
| Subtraction Phrases |
x minus two seven less than t |
x − 2 t − 7 |
| seven less t 5 subtracted from d *the difference between y and 4 m decreased by 3 |
7 − t d − 5 y − 4 m − 3 |
|
| Multiplication Phrases |
10 times t | 10t |
| one-half of x | 1/2 x | |
| *the product of y and z | yz | |
| 11 multiplied by y | 11y | |
| twice n | 2n | |
| Division Phrases |
x divided by 12 |
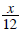 |
| the ratio of t to nine |
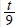 |
|
| *the quotient of y and z |
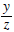 |
|
| Powers | the square of x |
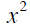 |
| the cube of z |
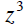 |
Example 1 Translate each into a variable expression.
a. The total of five times b and c.
b. Five times the total of b and c.
c. The quotient of eight less than n and fourteen.
d. Thirteen more than the sum of seven and the square of x.
e. Eighteen less than the cube of x.
f. Eighteen less the square of x
g. y decreased by the sum of z and nine.
h. The difference between the square of q and the sum of r and t.
2.3.2 Translate into a variable expression
Example 2 Translate each of the following into a
variable
expression.
a. Translate “a number multiplied by the total of six and
the cube
of the number.”
b. Translate “a number added to the product of five and
the
square of the number.”
c. Translate “the quotient of twice a number and the
difference
between the number and twenty.”
d. Translate “the product of three and the sum of seven
and twice
a number.”
2.3.3 Translate into a variable expression, and then
simplify the variable expression.
Example 3 Translate and simplify each expression.
a. Translate and simplify “the total of four times a
number and
twice the difference between the number and eight.”
b. Translate and simplify “a number minus the difference
between twice the number and seventeen.”
c. Translate and simplify “the difference between five
eighths of
a number and two thirds of the number.”
d. Translate and simplify “the sum of three fourths of a
number
and one fifth of the number.”
2.3.4 Defining Variables
Example 4
For each of the following define a variable and
express all unknown quantities in terms of that
variable.
a. The length of a swimming pool is 20 feet longer than
the
width. Express the length of the pool in terms of the width.
b. An older computer takes twice the amount of time to
process
data as a new computer. Express the amount of time it takes
the older computer to process the data in terms of the amount
of time it would take the new computer.
c. A guitar string 6 ft long was cut into two pieces. Use
one
variable to express the lengths of the two pieces.
d. If the sum of two numbers is 10. Use one variable to express
each number.
e. An investor divided $5000 into two accounts, one a
mutual
fund and the other a money market fund. Use one variable to
express the amounts invested in each account.


