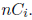Facts to Remember
1. Properites of Inequalities:
(a) If x < y and y < z then x < z.
(b) If x < y then x +z < y + z.
(c) If x < y and z is positive, then x z < y z.
However, if x < y and z is negative, then x z > y z.
(d) |x| < y if and only if −y < x < y.
(e) |x| > y if and only if either x > y or x < −y.
2. Properties of Exponents: Be aware that there are some natural
assumptions a
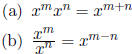
In particular,
x0 = 1 and 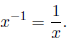
.
(c) 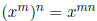
(d) These are obtained by combining the above rules:
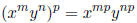 and
and
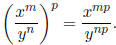
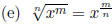
3. The determinant of a 2 by 2 matrix: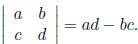
4. Cramer’s Rule: To solve the system of equations
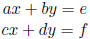
first calculate:
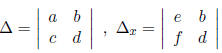 and
and
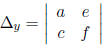
If Δ ≠ 0 then the system has a unique solution
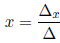 and
and
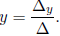
If Δ = 0 and one of Δx, Δy is non
zero, then the system is inconsistent i.e. has no
solution!
If Δ = Δx = Δy = 0, then the equations are essentially the
same and have infinitely
many solutions, provided at least one term with the variables is present.
5. The distance between two points A and B on the real line is d
(A,B) = |A − B|.
6. The distance between two points 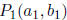 and
and 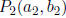 in the xy-plane: is
in the xy-plane: is
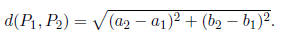
7. For two points 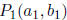 and
and
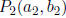 , the midpoint is
, the midpoint is 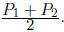
This evaluates to:
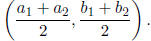
8. For the line containing two points
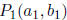 and
and 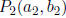 , a
parametric two point
, a
parametric two point
form is
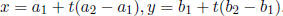
9. For the line containing two points
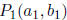 and
and 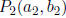 , a
compact parametric
, a
compact parametric
two point form is
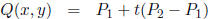 or
or
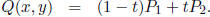
10. For the line containing two points
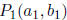 and
and 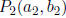 , the
two point form is
, the
two point form is
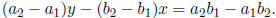
11. For the line containing two points
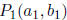 and
and 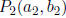 , the
slope is
, the
slope is
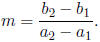
Further, the slope intercept form of the line is
y = m x + c,
where m is the slope and c is the y-intercept given
by
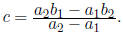
12. If p is the x-intercept and q is the
y-intercept of a line, then the intercept form
of the line is
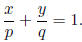
13. The equation of a circle with center at (a, b) and of radius r is
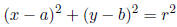
14. A parametric form of a circle centered at the origin and of radius r:
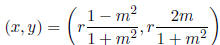
where m is the parameter.
15. The quadratic formula for solutions to ax2 + bx + c = 0, when a ≠ 0, is
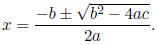
16. Trigonometric Functions:
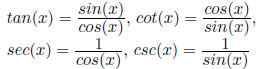
17. Trigonometric Identites:
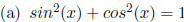 Fundamental
Identity.
Fundamental
Identity.
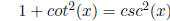 Variant 1.
Variant 1.
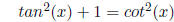 Variant 2.
Variant 2.
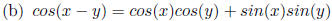 Basic Identity.
Basic Identity.
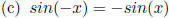 That is, Sine is
odd.
That is, Sine is
odd.
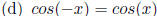 That is, Cosine is
even.
That is, Cosine is
even.
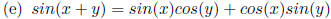 Addition rule for
sine.
Addition rule for
sine.
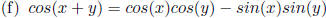 Addition rule for
Cosine.
Addition rule for
Cosine.
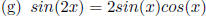 Double angle formula
for Sine.
Double angle formula
for Sine.
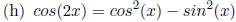 Double angle formula
for Cosine.
Double angle formula
for Cosine.
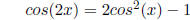 Variant 1.
Variant 1.
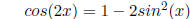 Variant 2.
Variant 2.
18. Derivative Formulas:
(a) If f(x) = p, where p is a constant, then f' (x) = 0.
(b) Power rule If 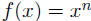 , then
, then
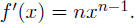
(c) If c is a constant and g (x) = c f (x) then g' (x) = c f' (x).
(d) Sum rule 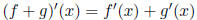
(e) Product rule If 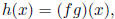 then
then 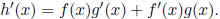
(f) Chain rule 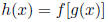 then
then
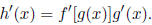
19. Linear Approximation:
Linear approximation to f (x) at x = a:
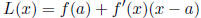
20. Newton’s Method for finding a root x = a of f
(x):
Start with a guess x = a and improve it to
Guess: x = a Improve to 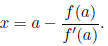
21. Combinations of n objects taken r at a time are given by:
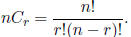
22. The Binomial Theorem:
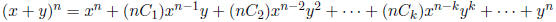
Thus, the coefficient of
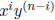 is simply
is simply