GEOMETRY DEFINITIONS

Perpendicular Two lines are called perpendicular if they form a right angle.

Congruent Triangles Two triangles ΔABC and ΔDEF are congruent (written
ΔABC 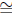ΔDEF) if all three corresponding angles and all three corresponding
sides are equal.

Similar Triangles Two triangles ΔABC and ΔDEF are similar (written
ΔABC ~ ΔDEF) if all three corresponding angles are equal.

Parallel Lines Two lines are parallel if they do not intersect.

Midpoint of a line segment The midpoint of a segment AB is the point M on the
segment for which MA = MB.

Angle bisector The bisector of an angle is the line that goes through the vertex of the
angle and splits the angle into two equal parts.

Parallelogram A quadrilateral is a parallelogram if the opposite sides are parallel.

Rectangle A quadrilateral is a rectangle if it has four right angles.

Square A quadrilateral is a square if it has four equal sides and four right angles.

Isosceles A triangle with two equal sides is called isosceles.

Distance from a point to a line The distance from a point P to a line m is de ned
to be the length of the line segment from P to m which is perpendicular to m.

Definition of concurrent lines Three lines are concurrent if they meet at a single
point.

Definition of perpendicular bisector The perpendicular bisector of a line segment
is the line that goes through the midpoint and is perpendicular to the segment.

Definition of circumcenter The point where the three perpendicular bisectors of the
sides of a triangle meet is called the circumcenter of the triangle.

Definition of incenter The point where the three angle bisectors meet is called the
incenter of the triangle.

Definition of altitude An altitude of a triangle is a line that goes through a vertex of
the triangle and is perpendicular to the opposite side.

Definition of orthocenter The point where the three altitudes meet is called the or-
thocenter of the triangle.

Definition of median A median of a triangle is a line that goes through a vertex of
the triangle and through the midpoint of the opposite side.

Definition of centroid The point where the three medians meet is called the centroid
of the triangle.

Definition of collinear Three points are said to be collinear if they all lie on the same
line.

Definition of signed ratio Let ℓ be any line and let C", A and B be three points on
ℓ. Make ℓ into a number line by choosing an origin and a positive direction and let
c', a and b be the coordinates of C", A and B. We define

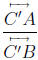
to be 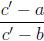and we call this a signed ratio.

Definition of circle A circle consists of all of the points which are at a given distance
(called the radius) from a given point (called the center).

Definition of tangent line A line is tangent to a circle 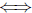it intersects the circle in
exactly one point.

BASIC FACTS

BF 1 SSS: if two triangles have three pairs of corresponding sides equal, then the tri-
angles are congruent.

BF 2 SAS: if two triangles have two pairs of corresponding sides and the included angles
equal, then the triangles are congruent.

BF 3 ASA: if two triangles have two pairs of corresponding angles and the included side
equal, then the triangles are congruent.

BF 4 If two triangles are similar then their corresponding sides are proportional: that
is, if ΔABC is similar to ΔDEF then

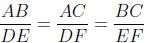
BF 5 If two parallel lines ℓ and m are crossed by a transversal, then all corresponding
angles are equal. If two lines ℓ and m are crossed by a transversal, and at least one
pair of corresponding angles are equal, then the lines are parallel.

BF 6 The whole is the sum of its parts; this applies to lengths, angles, areas and arcs.

BF 7 Through two given points there is one and only one line. (This means two things.
First, it is possible to draw a line through two points. Second, if two lines have
two or more points in common they must really be the same line).

BF 8 On a ray there is exactly one point at a given distance from the endpoint. (This
means two things. First, it is possible to find a point on the ray at a given distance
from the endpoint. Second, if two points on the ray have the same distance from
the endpoint they must really be the same point.)

BF 9 It is possible to extend a line segment to an infinite line.

BF 10 It is possible to find the midpoint of a line segment.

BF 11 It is possible to draw the bisector of an angle.

BF 12 Given a line ℓ and a point P (which may be either on ℓ or not on ℓ) it is possible
to draw a line through P which is perpendicular to ℓ.

BF 13 Given a line ℓ and a point P not on ℓ, it is possible to draw a line through P
which is parallel to ℓ.

BF 14 If two lines are each parallel to a third line then they are parallel to each other.

BF 15 The area of a rectangle is the base times the height.