Math 131 Test questions
Important:
 Show your work. A sole answer without anything to show that you honestly solve
the problem will be graded zero.
You can use a calculator, but only to help you in calculating or checking your
work. Simply copying answer from
calculator will be considered cheating (for example, input a quadratic equation
in a scientific calculator and copy its
solution).
You can use a print of the online lecture note, NOT YOURS, so it can be
considered fair for all students. Along with
the note, you can also bring a small cheat-sheet (not a A4 sized one).
I DO give partial credits, at my standard. This means, writing some weird
stuff and claim it solved the question
doesnt mean you will get some credits.
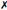I prefer you give answer in rational value or radical form, a decimal answer
(like, 2.6458 in stead of 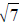 ) is ugly
and in some situation will not be acceptable.
No make-up test !!! except super extraordinary reason.
Dont forget to write your name on the first page of your work, or on this sheet
and staple to your papers. Also
remember to write your name on the back of the last sheet which helps me in
returning your tests later.
Test questions:
Problem 1: 5 points
Find the domain of the following function:
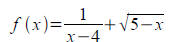
Solution:
We need x−4≠0 and 5−x≥0 , which means x≤5 and x≠4
Problem 2: 5 points
You are going to make a rectangle and a square from a 100 feet colorful string.
The shapes are
described as below. Suppose the rectangle is about to be created first, with
size x and 3x.
Express the area of the square as a function of x.
 
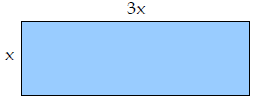
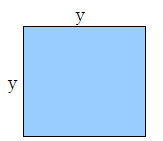
If the size of the rectangle is 10x30 (that is, x = 10), how big is the square
(what is its area)?
Solution:
The perimeter of the rectangle is 2(x+3 x)=8 x , hence whats left to make the
square is
4y = 100 – 8x, which yields y = 25 – 2x. This leads to the expression of the
area of the square:
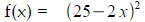 . When x = 10, we have area =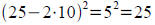
Problem 3: 5 points
You are given a quadratic function: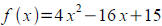 and its graph is a
parabola (P)
[a] (1 point) Find the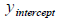 of P and y axis
[b] (2 points) Find the two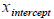 's of P and x axis ( that means, solve
f(x) = 0 )
[c] (2 points) Find the equation of the line which goes through the vertex of P
and is parallel
with the line y = 4 x
Solution:
[a] 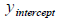: (0 , 15)
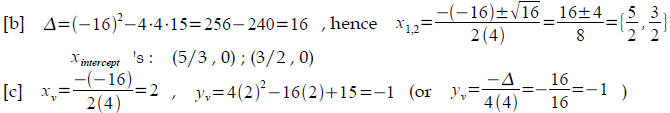
The line is parallel to y = 4x, so it must be y = 4(x-2) – 1 = 4 x – 9
Problem 4: 5 points
Given a function: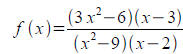 
. Compute the following limits:
[a] (1 point)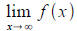 
[b] (1 point)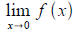 
[c] (3 points)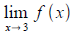 
Solution:
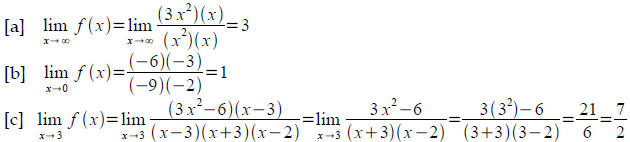
Problem 5: 10 points
Use Least Square method to find the equation of the line that best fits the
following data:
(1 , 1) ; (2 , 4) ; (3 , 5) ; (4 , 9) ; (5 , 11)
Solution:  ,m=5/2 , b=−3 /2 , y=2.5x−1.5
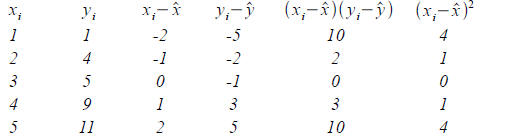
Problem 6: 5 points
Compute the derivative of the following function:
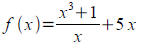
Solution:
f(x)=x2+x-1+5 x therefore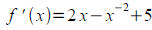
Bonus question: 5 points
Find the equation of the line which is tangent to the graph of y = f(x) at x = 1
Solution:
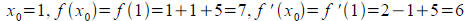
Equation of tangent line: y=6(x−1)+7=6 x+1
Problem 7: 5 points
Find the derivative of: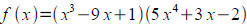 
Solution:
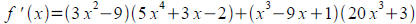
Extra credit question: 5 points:
Approximate: 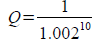 . Show details.
Solution:
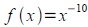 , x=1, h=0.002 , f (1)=1 , also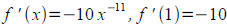
Therefore, Q= f (x+h) ≈ f (x )+h f ' (x)=1+0.002 (−10)=1−0.02=0.98
|