Linear Equations and Formulas

The Algebra Pyramid

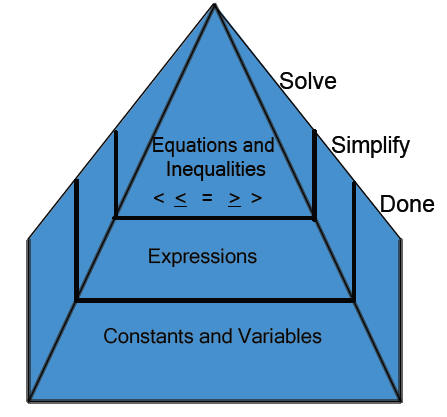
Definitions:
Solution: A number that makes an
equation true when it replaces the
variable in the equation.

Solution set: A set containing all the
solutions for a given equation.

Linear equation in one variable: An
equation with only one variable; the
variable is not raised to a power.

Identity: An equation in which every real
number (for which the equation is
defined) is a solution.

Contradiction: An equation that has no
solution.

Addition Principle of Equality:
If a=b, then a+c=b+c is true for all real numbers a, b, and c.
(If an equation is true and the same number is added to both sides, the equation is still
true.)

Multiplication Principle of Equality:
If a=b, then ac=bc is true for all real numbers a, b, and c, where c=0.
(If an equation is true and both sides are multiplied by the same number, the equation
is still true.)

Pattern for solving linear equations in 1 variable:

Get it READY to solve:
1. Distribute to clear parentheses
2.Multiply to clear fractions and decimals
3. Combine like terms.

Now it is ready, so SOLVE it:
1. Get variable on only one side
using addition principle
2. Get constants on the other side
using addition principle
3. Eliminate the coefficient of the variable
using multiplication principle.

Now you've solved it, so CHECK it.
1. Substitute the possible solution for the variable
2. Simplify both sides
3. If the result is true, it is a solution
If the result is false, it is not a solution.

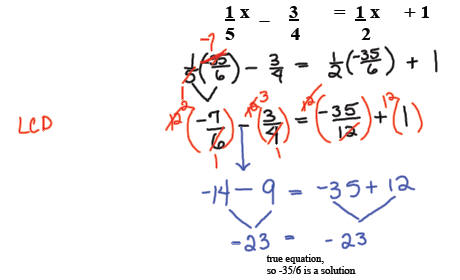
solve

solve

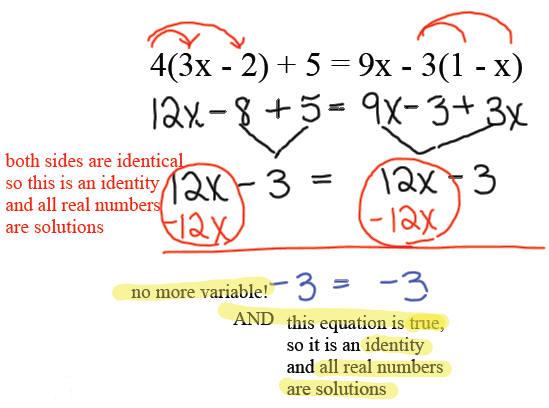
solve

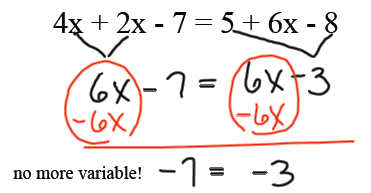
AND this equation is FALSE
so this is a contradiction and
has no solution

Pattern for clearing fractions:
1. Find one LCD for the entire equation.
2. Multiply every term in the entire equation
by that LCD, even if the term does not contain
a fraction. All denominators should cancel out.
3. Solve the remaining equation.

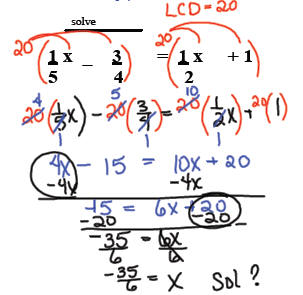
In certain situations you can clear fractions by multiplying by the reciprocal of the fraction.
However, the equation must be in the right form and you must avoid common careless mistakes.
Clearing fractions, as instructed above, will always work.

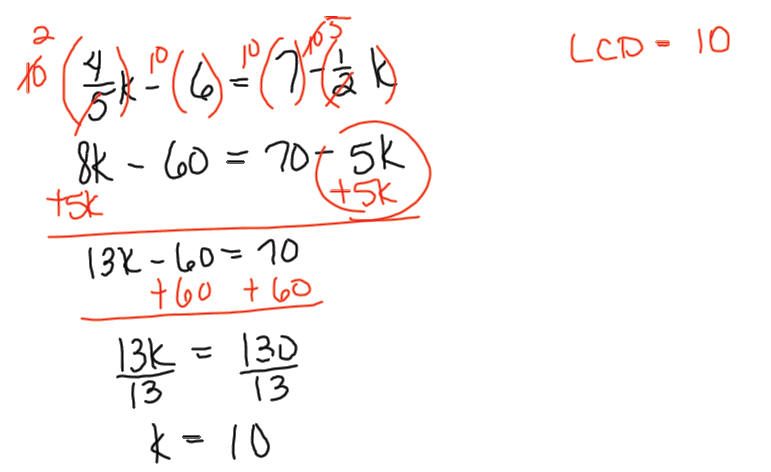
Pattern for clearing decimals:
1. Find one LCD for the entire equation.
It will be a power of 10.
2. Multiply every term in the entire equation by that LCD,
even if the term does not contain a fraction.
All denominators should cancel out.
3. Solve the remaining equation and check.

Instructions?
0.4 (n - 3) = 0.25n + 6

To isolate a particular variable in a formula:
1. Treat all other variables as constants.
2. Isolate the desired variable using the pattern for solving equations.

P = R - C solve for R
I = Prt  solve for r
P = 2l + 2w solve for w
C = 5/9 (F - 32) solve for F