Review of Chapter 1

Operations Involving Fractions

Order of Operations
The acronym PEMA is commonly used to help students remember the order of operations.
P = parentheses or any grouping symbols
E = exponents
M = multiplications or divisions (evaluate in the order in which they occur, working from left to right)
A = additions or subtractions

Example: Simplify 5[(3 +1)² ÷ 8× 2]

Exponents

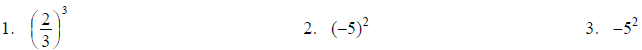
Types of Numbers

· REAL NUMBER = Any number on the number line.
Examples:

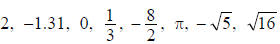
· NATURAL NUMBERS = 1, 2, 3, 4, 5, 6, ...
Examples:

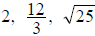
· WHOLE NUMBERS = 0, 1, 2, 3, 4, 5, 6, ...
Examples:

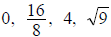
· INTEGERS = ..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...
Examples:

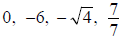
· RATIONAL NUMBER = Any number that can be written in the form a/b where a,b are integers and b≠0.
Notes: (a) Terminating decimals are rational numbers.
(b) Repeating decimals are rational numbers.

Examples: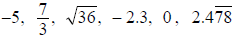

· IRRATIONAL NUMBER = Any real number that is not rational.
Note: Decimals that are simultaneously nonterminating and nonrepeating are irrational numbers.

Examples:

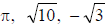
NOTE: The rational numbers together with the irrational numbers comprise the real numbers.

Absolute Value
The absolute value of a number is the distance between the number and 0 on a number line.
1. |7|
2. |-3|
3. -|-2 + 5|

Important Division Facts
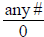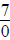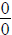·  is undefined. Examples: and are undefined.

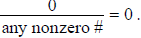·   Example: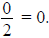
 

Addition and Subtraction of Real Numbers

Example: Simplify [-4 - (-6)] - (-1 - 5) + (3 - 9)

Properties of the Real Number System
Let a,b,c be real numbers.
· COMMUTATIVE PROPERTY:
a + b = b + a
ab = ba

The commutative property states that the order in which two numbers are added or multiplied does not
affect the result.
Example: 2(7) = 7(2)

· ASSOCIATIVE PROPERTY:
(a + b) + c = a + (b + c)
(ab)c = a(bc)

The associative property states that when adding or multiplying three numbers, the same result is obtained
whether the first two numbers are grouped together or the last two numbers are grouped together.
Example: (2 + 3) + 4 = 2 + (3 + 4)

· DISTRIBUTIVE PROPERTY:
a(b + c) = ab + ac
a(b - c) = ab - ac
Examples: Use the distributive property to rewrite each expression.
1. 3(x + 5)
2. 4(3a - b)
3. -2(4k - 7)
4. -(-3 + 2z)

Important Definitions
1. A term is a number (constant), a variable, a product, or a quotient.
Examples: 5, x, 4x³y, and 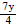are examples of terms. 3x - y + 7 has 3 terms (3x, -y, and 7).

2. The numerical part of a term is called its coefficient.
Example: The coefficients of the terms of 3x - y + 7 are 3, -1, and 7.

3. Like terms are terms that have the same variables with the same exponents.
Examples: 4x³ and -7x³ are like terms. 8y² and 3y are unlike terms.

Simplifying Expressions by Combining Like Terms

1. 7x² + 2x² - 8y² + 3x
2. 4 - 3(x - 5) + 2x
3. -(5y + 2) + 2(3 - y) - 8