MATH 701 Quadratics Solutions
1. Compute the distance between the following pairs of points.
(a) (3, 4) and (−10, 6)
Answer: : sqrt (173)
(b) (−3,−8) and (−3, 12)
Answer: : 20
2. Find the focus, directrix, vertex, and axis of symmetry of each of the
following parabolas.
(a) y = 3.2x^2
Answer: : The focus is (0, .078); the directrix is y = −.078; the
vertex is (0, 0); the axis of symmetry is x = 0.
(b) y = −4.5x^2
Answer: : The focus is (0,−.0556); the directrix is y = .0556; the
vertex is (0, 0); the axis of symmetry is x = 0.
(c) y = 2x^2 + 6
Answer: : The focus is (0, 6.125); the directrix is y = 5.875; the
vertex is (0, 6); the axis of symmetry is x = 0.
(d) y = 3x^2 − 5
Answer: : The focus is (0,−4.917); the directrix is y = −5.083;
the vertex is (0,−5); the axis of symmetry is x = 0.
(e) y = 4(x − 2)^2 + 15
Answer: : The focus is (2, 15.0625); the directrix is y = 14.9375;
the vertex is (2, 15); the axis of symmetry is x = 2.
3. Let f(x) = −3x^2.
(a) What is the equation whose graph is the graph of y = f(x) shifted
to the left four units?
Answer: : y = −3(x + 4)^2 = −3x^2 − 24x − 48
(b) What is the equation whose graph is the graph of the equation
from part (a) shifted up six units?
Answer: : y = −3(x + 4)^2 + 6 = −3x^2 − 24x − 42
4. Find the x- and y-intercepts of the function f(x) = −3x^2 + 17x + 90.
Answer: : The x-intercepts are (9, 0) and (−10/3, 0). The y−intercept
is (0, 90).
5. A fluorescent bulb hangs below a parabolic reflecting shade. The bulb
is 1/2 inch in diameter and must have one inch of clearance between
the top of the bulb and the shade and between the bottom of the bulb
and the bottom edge of the shade.
(a) Write an equation for the parabolic curve of the reflector and give
the coordinates of the focus.
Answer: s here may vary. I put the vertex of the parabola
at (0, 0), which makes the focus (0,−5/4) and the equation y =
−x^2/5.
b) What is the diameter of the shade opening?
Answer: :
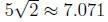inches.
6. Factor the quadratic 2x^2 − 8x − 42.
Answer: : 2x^2 − 8x − 42 = 2(x − 7)(x + 3)
7. Expand the product (3x − 1)(x + 5).
Answer: : (3x − 1)(x + 5) = 3x^2 + 14x − 5
8. For each of the following quadratic polynomials, find the vertex, the
axis of symmetry, the y − intercept, and the roots.
(a) 47 − 2x − 7x^2
Answer: :
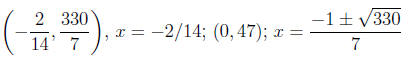
(b) 4x^2 − 18x − 5
Answer:
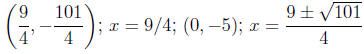
9. A bullet is fired straight up into the air from a rooftop 100 feet off the
ground with an initial velocity of 2800 feet per second.
(a) How high does the bullet go?
Answer: : 122,600 feet or 23.22 miles
(b) How long does it take the bullet to reach its highest point?
Answer: : 87.5 seconds
(c) How long does it take the bullet to fall back to the ground?
Answer: : 175.036 seconds
(d) How fast is the bullet travelling when it hits the ground?
Answer: : 2801.15 feet per second
10. Solve the equation 2x^2 − 5x = 17 − 2x^2 + x.
Answer: :
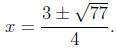
11. Write the equation of the parabola with vertex (2, 3) that passes through
the point (4,−1). Put the equation in the form y = ax^2 + bx + c.
Answer: : y = −(x − 2)^2 + 3 = −x^2 + 4x − 1.
Extra.
12. For the function f(x) in the preceding example, calculate a formula for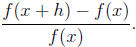
What does this quantity represent? What happens as h -> 0?
Answer: : 2 + h + 2x; this represents the average rate of change of the
function over the interval [x, x + h]; it approaches 2 + 2x.
13. Show that the axis of symmetry of a parabola really is an axis of
symmetry.
That is, if x1 is a point r units to the right of the axis of
symmetry and x2 is a point r units to the left of the axis of symmetry,
show that f(x1) = f(x2).
14. Let f(x) = ax^2 + bx + c. The tangent line to the graph of y = f(x)
at a point x = r is the line that passes through the point (r, f(r)) and
whose rate of change is equal to the limiting average rate of change of
f(x). Find the equation of the tangent line to the graph of y = f(x)
at the point x = r.
15. The focus of the parabola y = ax^2 is the point (0, a/4), and the
directrix
is the line y = −a/4. Show that if P = (x, y) is any point on
the graph of the parabola, then P is equidistant from the focus and the
directrix. This is a geometric way of defining a parabola.
16. By shifting a parabola of the form y = ax^2, find the focus and directrix
of the parabola y = 2x^2 − 3x + 7.