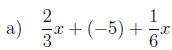HOMEWORK 05 SELECTED SOLUTIONS

Exercise 5.2. You have a party tonight, so you decide to buy beer and pork
(for BBQ) in a grocery store. According to the price tag, you have to pay b
dollars for beer and p dollars for pork. Assume that beer is taxable (Texas
state tax is 8.25%, it is equivalent to the factor 0.0825), and beef is tax free.

a) Which algebraic expression represents the tax you pay?
b) Which algebraic expression represents the price of your purchase before tax?
c) What is the total price of your purchase?
d) Assume that b = 20 and p = 15. Plug these values into a), b), and c).

Solutions. You pay b+p dollars for beer and pork before tax and 0.0825 · b
dollars as state sale tax. The total price is 1.0825 · b + p dollars.

If b = 20 and p = 15 then the price before tax is 35 dollars, the tax is
0.0825 · 20 = 1.65 dollars. The total amount is 36.65 dollars.

Exercise 5.3. Determine whether the value(s) is(are) a solution to the equation.

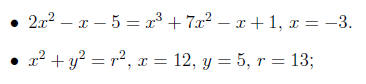
a). Plugging x = −3 we get 16 = 40, which is, of course, false. Thus, x = −3
is not a solution of the above equation.

b). Plugging the numbers, we get 169 = 169, which is true. Thus, this triple
is a solution.

Exercise 5.4. Simplify the algebraic expression by combining like terms.

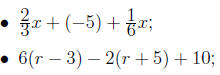
	= combine like terms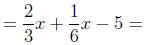
	simplifying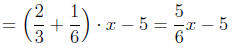

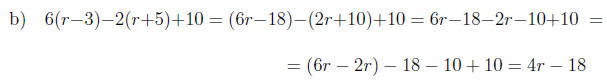
Exercise 5.5. Solve the linear equation

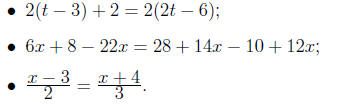
Solution. a)

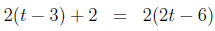	open parenthesis
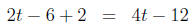	simplifying
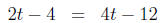	moving t to the LHS
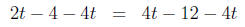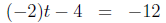	adding 4 to both sides

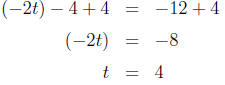Exercise 5.6. A 20 lb bag of grass seed will cover an area of 10000 ft².

• How many pounds are needed to cover an area of 140000 ft²?
• How many bags of grass seed must be purchased to cover an area of 140000 ft²?

Solution. Let x be the weight of grass seeds (in pounds) needed to cover 140000 ft². Then, we get the relation

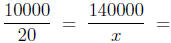
area which can be covered with 1 lb

which is equivalent to

10000 · x = 140000 · 20

from which we conclude

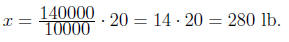
The number of bags is

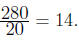
Exercise 5.9. (Temperature conversion). The temperature K (absolute/Kelvin
scale) and the temperature F (Fahrenheit scale) are related with the formula

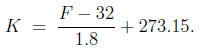
• Use google/wikipedia website to find out what does 0 degrees K rep-
resent. Are there negative temperatures in K? Are there negative
temperatures in F?
• Find F when K = 0 (absolute zero);
• Find K when F = 100;

Solution. Kelvin scale is an absolute scale and 0 K is the lowest possible
temperature in our world. Therefore, if you see negative Kelvin temperature,
then there is a mistake. In Fahrenheit scale, negative scales are possible.

Plugging K = 0 into the equation we get

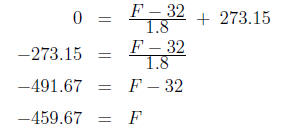
Thus, there are no temperatures less than −459.67 degrees on the Fahrenheit scale.

Plugging F = 100 we get

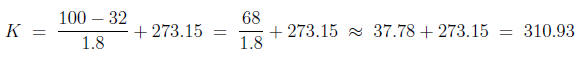
Exercise 5.10. (Weight gain/loss). A person’s body mass index (BMI) is
found by formula

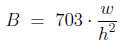
where w is the person’s weight (in pounds), and h is the person’s height (in
inches). Lance Bass is 6 ft tall and weighs 200 lb.

a) Read wikipedia about BMI. Indicate when person is underweight, over-
weight, or have an optimal weight.
b) Determine Lance’s BMI.
c) Use wikipedia chart to see in which category the Lance’s weight is.
d) If Lance would like to have BMI of 20, how much weight would he need to gain/lose?
e^*) Find/estimate your weight and your height, compute your BMI. Which
is your weight category? ^* Remark. Answer this part on a separate
sheet of paper, DO NOT turn it in.

Solution. According to the wikipedia chart, we have optimal weight if 18.5 ≤
BMI≤25. You are underweight if your body mass index is less than 18.5,
and you are overweight if this index is greater than 25.

Lance is 6 · 12 = 72 inches tall. Thus, his index is

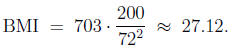
Thus, Lance is overweight.

Assume that Lance wants to have BMI = 20 then he must have the weight
w₂₀ satisfying

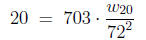
which is equivalent to w₂₀ = 20 · 72² ÷ 703 = 147.48. Therefore, Lance has
to loose 200 − 147.48 = 52.52 pounds :) . I guess Lance is an optimist.

Exercise 5.11.

a) Solve the equation 9x + 4z = 7 + 8y for y.
b) Solve the equation 9x + 4z = 7 + 8y for z.
c) Solve the equation S = πr^2 + πrs for s.
d) Solve the equation A = 1/2h(b₁ + b₂) for b₂.

Solution. Consider, for instance, parts c) and d).

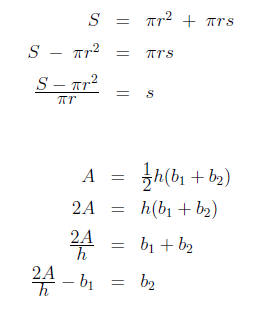
Exercise 5.13. Set up an equation that can be used to solve the problem.
Solve the equation and find the desired value.

a) Miguel Garcia purchases two pairs of pants at the Gap for $60. If one
pair was $10 more than the other, how much was the more expensive pair?

b) The Gilberts purchased a car. If the total cost, including 5% tax sales
tax, was $14,512, find the cost of the car before tax.

Solution. a). Let x denote the cost of the more expensive pair. Then, the
price of the other pair is x − 10 dollars. Then, we get the equation

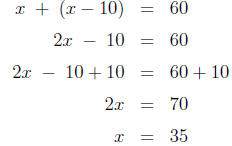
Thus, the more expensive pair costs 35 dollars. Less expensive pair is 35 − 10 = 25 dollars.

Solution. b). Let x denote the cost of the car before tax. Then, the sales
tax is 0.05x and the total cost of the car is x + 0.05x = 1.05x dollars. Thus,
we get the equation

1.05x = 14512

from which we get

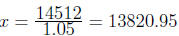dollars.