Functions II
Inverse
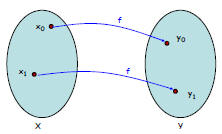
A function f: X → Y is called invertible if and only if
there exists a function g : Y → X such that
y = f(x) ↔ x = g(y) for all x ∈ X and for all y ∈ Y.
We call g the inverse of f and write g = f-1.
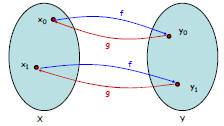
Theorem: A function f: X → Y is invertible if and only if
it is a bijection, and if f is invertible, then the inverse is
unique.
bijection → invertible
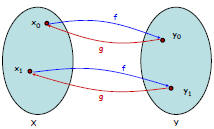
Theorem: A function f: X → Y is invertible if and only if
it is a bijection, and if f is invertible, then the inverse is
unique.
bijection → invertible

Bijection
Surjective: Everything
has an incoming arrow
(onto)
AND
Injective: Nothing has
more than one incoming
arrow (one-to-one)
We can construct an
inverse: if f(x) = y,
then g(y) = x.
Theorem: A function f: X → Y is invertible if and only if
it is a bijection, and if f is invertible, then the inverse is
unique.
bijection → invertible
¬bijection → ¬invertible
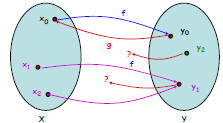
Not Bijection
Not Surjective:
Something does not have
an incoming arrow
OR
Not Injective:
Something has more than
one incoming arrow
In either case, we cannot
construct an inverse
Back to combinatorics...
The Bijection Principle: If A and B are finite sets and there is
a bijection from A to B, then |A| = |B|.
One way to count the number of elements in a set A is to show
that there is a bijection from A to some other set B and count
the number of elements in B.
How many subsets are there
(including the empty set) of
a set with n elements?
| How many subsets are there (including the empty set) of a set with 4 elements? 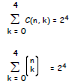 |
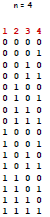 |
| There is a one-to-one correspondence between subsets and binary numbers of length 4, and we know that there are 16 such numbers. So by the Bijection Principle, there are 16 subsets. |
Combinations with Repetition
Consider 7 kinds of bills: $1, $2, $5, $10, $20, $50, $100
Problem: Suppose I have a bag with lots of bills in it, and I pull out 5 bills.
How many different combinations could there be?
Equivalent problem: Suppose I have 5 blank bills. How many ways can
I print denominations on them?
Equivalent problem: Suppose I have 7 empty bins, labeled with the
denominations. I'm going to place 5 blank bills in them, to
be printed later. How many ways can I distribute the 5 bills?
Equivalent problem: How many sets can I form by selecting 5 items,
with repetition allowed, from a set of 7 items?
Equivalent problem: How many integer solutions are there to the equation
x1 + x2 + x3 + x4 + x5 + x6 + x7 = 5 where 0 ≤ xi ≤ 5 ?
There is a one-to-one correspondence between solutions to one problem
and solutions to another.
Without answering either question, why do these two
questions
have the same answer?
• How many sets of size 2 can be made choosing elements
from {1, 2, 3, 4, 5, 6, 7, 8, 9}?
•How many sets of size 7 can be made choosing elements
from {1, 2, 3, 4, 5, 6, 7, 8, 9}?
Because every solution to one of the questions also specifies
a solution to the other.
{3, 8} <=> {1, 2, 4, 5, 6, 7, 9}
{5, 7} <=> {1, 2, 3, 4, 6, 8, 9}
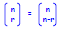
Functions
successor(n) = n + 1
sqr(x) = x2
sqr(successor(n)) = (n+1)2
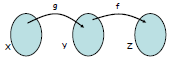
Functions
successor(n) = n + 1
sqr(x) = x2
sqr(successor(n)) = (n+1)2
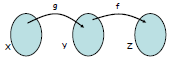
Let g be a function g : X → Y and f be a function f : Y →
Z.
A new function (denoted by f ° g) is defined by the following rule:
For all x ∈ X, (f ° g)(x) = f(g(x)).
This is called the composition of f and g.
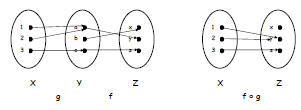
Is g ° f defined?

Is g ° f defined?
No, the co-domain of f is not the domain of g.
f : Y → Z g : X → Y
f(x) = 2x + 3
g(x) = 3x + 2
f ° g(x) = f(g(x)) = f(3x + 2) = 6x + 7
g ° f(x) = g(f(x)) = g(2x + 3) = 6x + 11
So composition is not commutative.
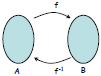
Suppose A is a set. The identity function on A is the function
lA : A → A such that for all x ∈ A, lA(x) = x.
So if f: A → B is a bijection, then
f-1 ° f is lA
and
f ° f-1 is lB
More Theorems
Theorem: The composition of functions is associative.
That is, suppose that functions f, g, and h are such that
h : A→B, g : B→C and f : C→D. Then f ° (g ° h) = (f ° g) ° h.
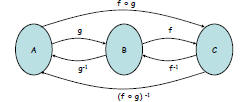
Theorem: If g : A→B and f : B→C are bijections, then
f ° g is a bijection and (f ° g)-1 = g-1 ° f-1
Theorem: If g : A→B and f : B→C are bijections, then
f ° g is a bijection and (f ° g)-1 = g-1 ° f-1
(f ° g) : A→C
(f ° g)(x) = f(g(x))
(f ° g) is a bijection is a iff every element of C has precisely one pre-image
If y ∈ C, then y has precisely one pre-image under f in B, call it y'
Since y' ∈ B, y' has precisely one pre-image under g in A, call it y''
y'' is the unique pre-image of y under (f ° g)
Functions
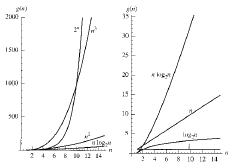
When you study the analysis of algorithms, the following functions
will be interesting, because they can often be used to characterize the
growth of running time based on the growth of the size of the data set.
f(n) = 1
f(n) = log n
f(n) = n
f(n) = n log n
f(n) = n2
f(n) = 2n
f(n) = n!