Greek Numbers and Arithmetic

1 Introduction

The earliest numerical notation used by the Greeks was the Attic system.
It employed the vertical stroke for a one, and symbols for“5”, “10”,
“100”, “1000”, and “10,000”. Though there was some steamlining of
its use, these symbols were used in a similar way to the Egyptian system,
being that symbols were used repeatedly as needed and the system was
non positional. By the Alexandrian Age, the Greek Attic system of
enumeration was being replaced by the Ionian or alphabetic numerals.
This is the system we discuss.

The (Ionian) Greek system of enumeration was a little more sophisticated
than the Egyptian though it was non-positional. Like the Attic
and Egyptian systems it was also decimal. Its distinguishing feature is
that it was alphabetical and required the use of more than 27 different
symbols for numbers plus a couple of other symbols for meaning. This
made the system somewhat cumbersome to use. However, calculation
lends itself to a great deal of skill within almost any system, the Greek
system being no exception.

2 Greek Enumeration and Basic Number Formation

First, we note that the number symbols were the same as the letters of
the Greek alphabet.

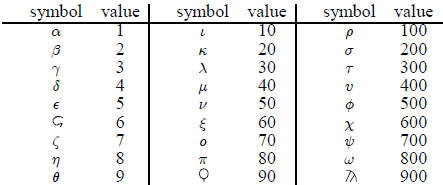
where three additional characters, the 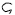(digamma), the 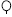(koppa),

and the 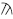(sampi) are used. Hence,

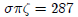
Larger Numbers

Larger numbers were also available. The thousands, 1000 to 9000,
were represented by placing adiacritical mark ' before a unit. Thus

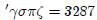
In other sources we see the diacritical mark placed as a subscript before
the unit. Thus

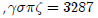
The uses of a M was used to represent numbers from 10,000 on
up. Thus

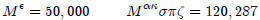
Alternatively, depending on the history one reads

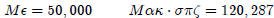
Archimedes, in his book The Sand Reckoner, calculated the number
of grains of sand to fill the universe. This required him to develop
an extention the power of Greek enumeration to include very large
numbers.

Fractions

In the area of fractions, context was crucial for correctly reading a
fraction. A diacritical mark was placed after the denominator of the
(unit) fraction. So,

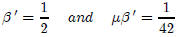
but this latter example could also mean .

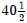More complex fractions could be written as well, with context again
being important. The numerator was written with an overbar. Thus,

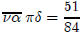
Numerous, similar, representations also have been used, with increasing
sophistication over time. Indeed, Diophantus uses a fractional
form identical to ours but with the numerator and denominator in reversed
positions.

3 Calculation

The arithmetic operations are complex in that so many symbols are
used. However, as you can imagine, addition amounts to grouping and
then carrying. For exampl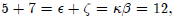e not terribly unlike
what we do. Multiplication was carried out using the distributive law.
For example:

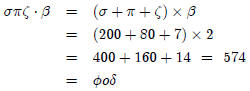
Remarkably, division was performed in essentially the same way as we
do it today.