Introduction to Quadratic Functions

A. Definition

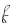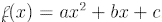is a quadratic function if where a≠0

The graph is a parabola

B. Parabolas

1. Parabolas

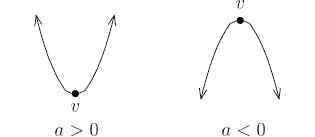
2. v is the vertex of the parabola

C. Formula for the Vertex

1. Vertex Formula: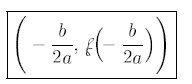

2. See MTH103: College Algebra for the justification of this formula

D. Graphing Quadratic Functions (Parabolas)

1. Locate the vertex: use the vertex formula
2. Find the x and y intercepts.
3. Plot the points and connect in a smooth curve, recognizing whether it opens up or down.

E. Examples of Graphing

Example 1: Graphwhere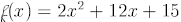

Solution
1. Locate vertex:

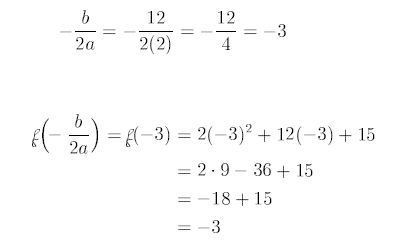
Vertex Formula:

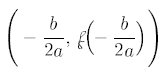
Thus the vertex is (-3,-3)

2. Intercepts
y-intercept:

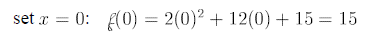
x-intercept:

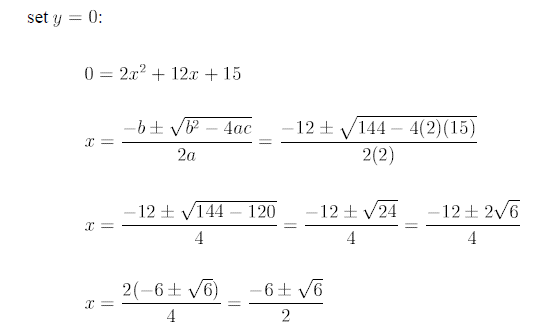
3. Note the graph opens upward:

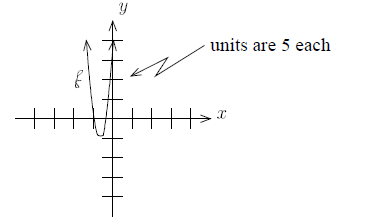
Example 2: Graphwhere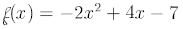

Solution
1. Locate vertex:

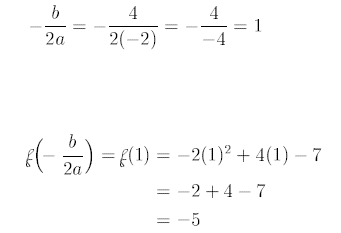
Vertex Formula:

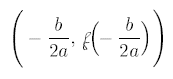
Thus the vertex is (1,-5)

2. Intercepts
y-intercept:

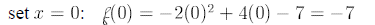
x-intercept:

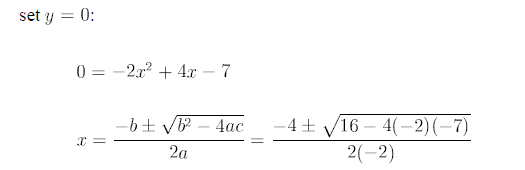
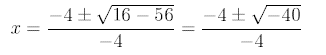
no real solutions!

Thus, no x-intercept

3. Note the graph opens downward:

F. Projectile Motion

A thrown object follows a parabolic path given by

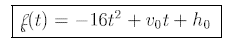
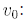initial upward speed

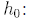initial height thrown from

Units of height: feet

The vertex is the peak of the path.

Features

1. The t-coordinate (“ x-coordinate”) of the vertex tells you
when the projectile reaches its maximum height

2. The “y-coordinate” of the vertex tells you what the maximum height is.

3. The projectile hits the ground when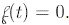

G. Projectile Motion Example

A ball is thrown upward with a speed of 16ft/s from a building 32 feet high.
What is the maximum height of the ball? When does it reach the ground?

Solution
Use the projectile motion model:

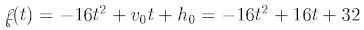
Now

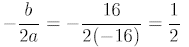
Also,

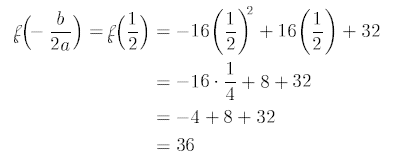
Thus the vertex is (1/2,36)

Now the maximum height is the y-coordinate of the vertex: 36 feet

The ball reaches the ground when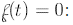

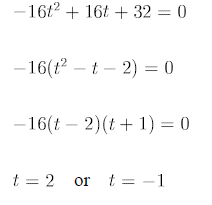
Since t=1 is not physical, we must have t=2 .

Thus the ball reaches the ground 2 seconds after being thrown.