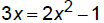Math 1051 Pre-calculus I Lecture Notes

Fri 30 Jan — A.6 Solving Equations

Activities:

Solving Equations:

Equation is two expressions set equal to each other.
To solve an equation means to find the values of the
variables in their domains that make the equation a true
statement. A solution satisfies an equation.

3 types of equations: Conditional, identity, contradiction
(Give Examples of each)

Solve these:

Solve:

 

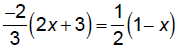
Use the standard procedure.
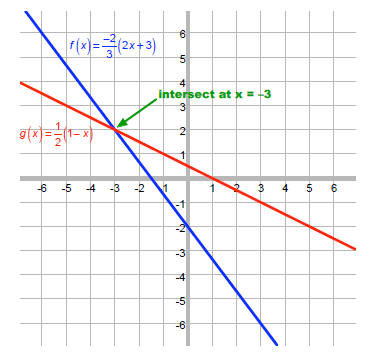
We can also solve this graphically. Since we want the value of x that makes these two expressions
equal, we could graph each and see where they intersect.
Rewrite this as follows:

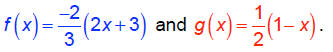
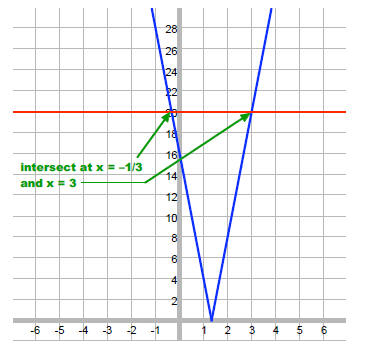
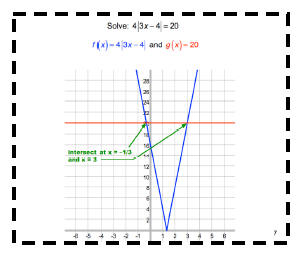
Find value of x where f(x) = g(x) on the graph:

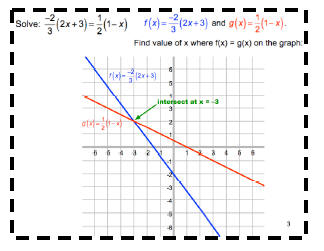
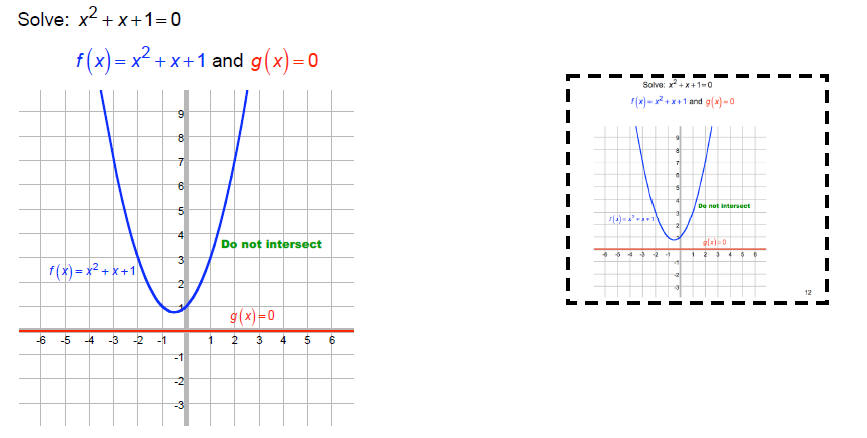
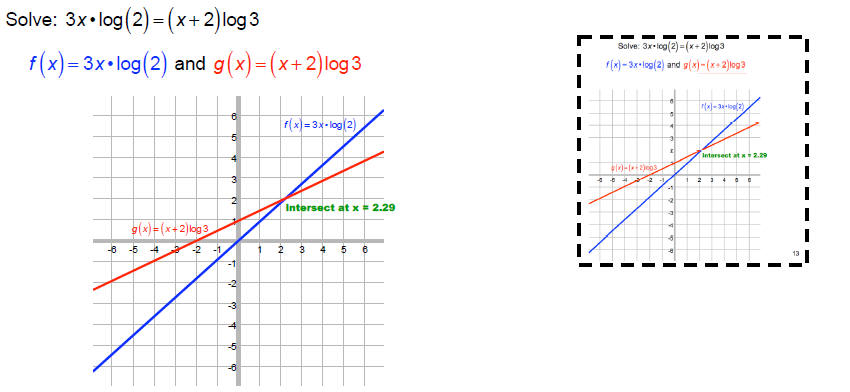
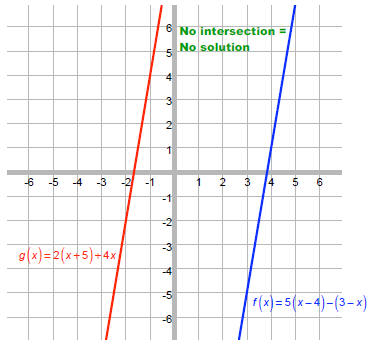
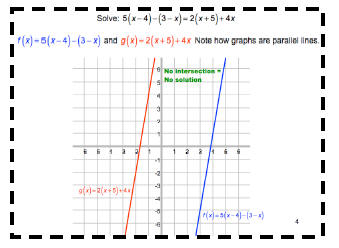
Solve:
5(x - 4) - (3 - x) = 2(x + 5) + 4x

ANS: Contradiction

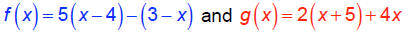
Note how graphs are parallel lines. No soln.

Solve:

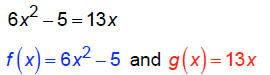
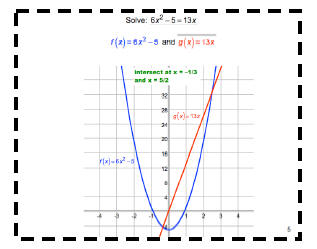
Solve:

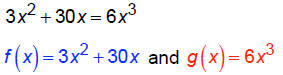
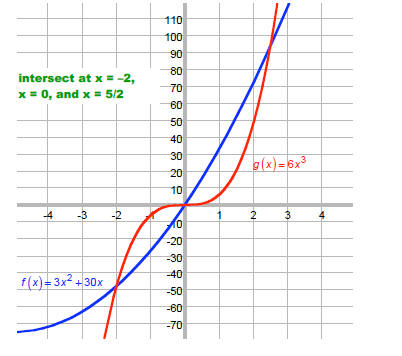
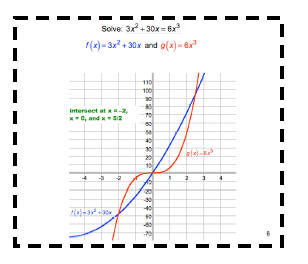
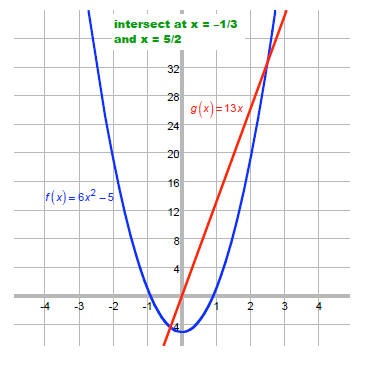
Solve:

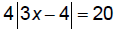
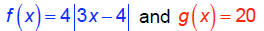
Solve:

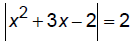
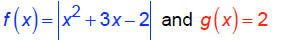
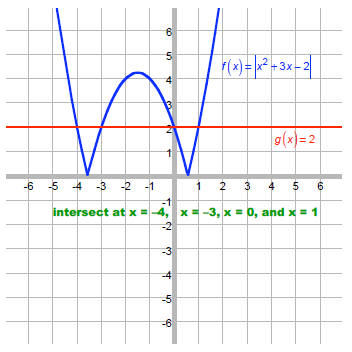
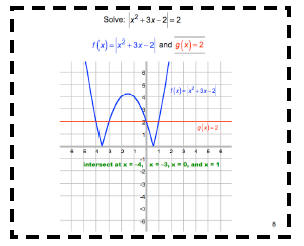
Solve:

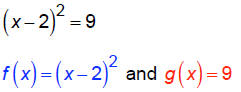
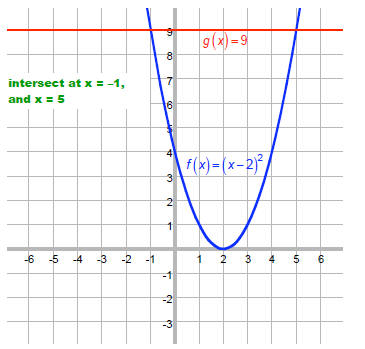
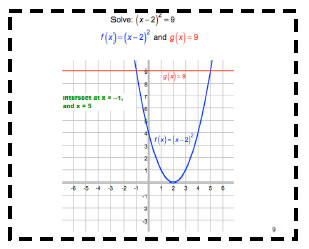
We can also solve a quadratic equation by Completing
the Square. All that means is that we construct a
perfect square from a given expression and then use
the square root method to solve.

To complete the square of x^2 + bx take half of b,
square this, and then add it to the expression.

For example, to make x^2 + 6x a perfect square we add

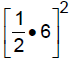
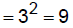
We get x^2 + 6x + 9 which can be written (x + 3)^2 , a perfect square.

Solve by completing the square:

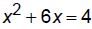
Solve by completing the square:

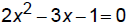
The standard form of a quadratic equation:
ax^2 + bx + c = 0 where a, b, c are real numbers
and a is not 0

We can use completing the square to solve this
to get the quadratic formula:

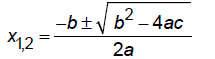
Solve using quadratic formula: