The Language of Mathematics Functions

1 Functions

1.1 Functions

Functions

•A function f from one set X to another set Y is a subset of the Cartesian
product X*Y such that for any x ∈X, there is exactly one y with (x, y) ∈f .

•Denote a function by f : X -> Y
•We usually write f (x) = y if (x, y) ∈f .
•The domain of f : X -> Y is X.
•The range of f : X -> Y is the set {y | (x, y) ∈f for some x ∈X}
Example.
1. f : R -> R given by f (x) = x² is a function.
2. Let X = {a, b, c} and Y = {v, c}. Then f = {(a, v), (b, c), (c, c)} is a
function.
3. g = {(v, a), (c, b), (c, c)} is not a function. (We call this a relation)

2 Specifying Functions

2.1 Arrow Diagrams

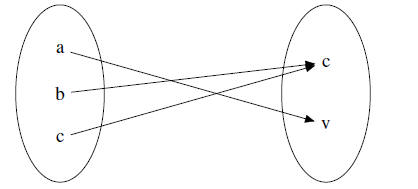
Arrow Diagrams

•For small enough functions, we can denote them with an arrow diagram
Example. Let X = {a, b, c}, Y = {v, c} and f = {(a, v), (b, c), (c, c)} as before.

2.2 Rules

Rules

•You are probably familiar with functions given by rules.
Example. 1. f (x) = x²
2. g(x) = e^x
3. h(x) = sin x

2.3 Graphs

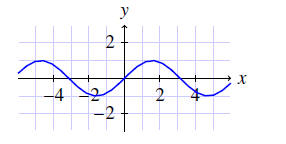
Graphs

•Suppose that f is a function whose domain and range are both subsets of R.
The graph of f is obtained by plotting each element of f as a point.
Example. The graph of f (x) = sin x

3 Specific Functions

3.1 Modulus Operator

Modulus Operator

•Recall Z denotes the set of integers.
•For x, y ∈Z with y > 0, define x mod y to be the remainder on dividing x
by y.
•x mod y is always nonnegative.

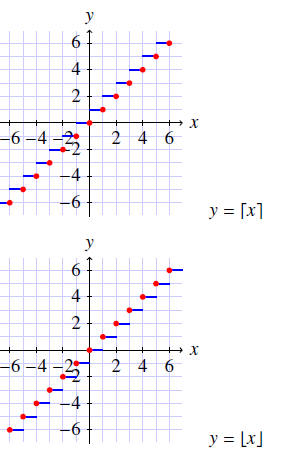
3.2 Floor and Ceiling Functions

Floor and Ceiling Functions

•The ceiling of a number, denoted 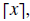is the least integer greater than or
equal to x. (Round up!)
•The floor of a number, denoted 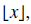is the greatest integer less than or equal
to x. (Round down!)

3.3 Operators

Operators
Let X be a set. A binary operator on X is a function X*X -> X (Two
inputs).
Let X be a set. A unary operator on X is a function X -> X.

Example. 1. If X is the set of all propositions in arithmetic, then 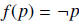is
a unary operator on X.

2. If U is a universal set, then f (A, B) = 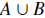is a binary operator on
3. f (x, y) = 3x - 2y is a binary operator on Z.

4 Properties of Functions

4.1 One-to-One Functions

One-to-One Functions

• A function f is one-to-one (or injective) if for each y ∈Y, there is at most
one x ∈X with f (x) = y.

4.2 Onto Functions

Onto Functions

• A function f is onto (or surjective) if for each y ∈Y, there is at least one
x ∈X with f (x) = y.

4.3 Bijective Functions and Inverses

Bijective Functions

•A function f is bijective if it is both one-to-one and onto.
•Bijective functions f have inverses f^-1

Inverses

•The inverse f^-1 of a bijective function “undoes” f
•Reverses the arrow diagram

Logarithms

•The function f (x) = lg x is the inverse of g(x) = 2x
•Called the base ∈logarithm of x
Example.

1. lg 64 = 6
2. lg 1000 ≈ 9.96578

4.4 Composition of Functions

Composition of Functions

•If g : X -> Y and f : Y -> Z are functions, we can define a new function
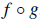, called the composition of f with g.
•Perform g, then f .
•The target of g and the domain of f must agree.

5 Hashing

5.1 Hashing

Hashing

•Want to organize stored data so that retrieval is efficient.
– Determine whether a particular item has been stored
– Edit or delete a particular item
– Find a place to insert a new item

•Hash tables are a commonly used method
– Have a hash function h : {Data} -> {Memory Locations}

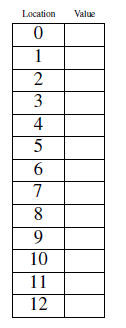
Suppose we have 6 students in a computing class, with student IDs:

We also have 13 memory locations, indexed 0 to 12.
Define a hash function by h(x) = x mod 13.

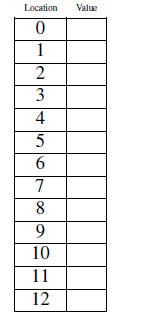
Suppose we now have 8 students in a computing class, with student IDs:

We may end up having a collision, i.e., two or more items trying to be placed in the same position.
We need a collision resolution policy. One simple one is simply to move to the next unoccupied
location.

Summary

Summary
You should be able to:
•Use functions and basic function terminology
•Identify functions using different methods
•Use the modulus operator and lg x
•Understand one-to-one and onto functions
•Understand and use hashing functions
•Deal with hashing collisions