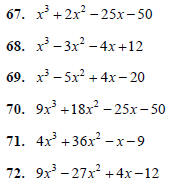Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Factoring Polynomials

At times, it can be difficult to tell whether or not a
quadratic of the form ax² + bx + c can be factored
into the form (dx + e)( fx + g) , where a, b, c, d, e, f,
and g are integers. If b² − 4ac is a perfect square, then
the quadratic can be factored in the above manner.

For each of the following problems,

(a) Compute b² − 4ac .

(b) Use the information from part (a) to
determine whether or not the quadratic can
be written as factors with integer coefficients.
(Do not factor; simply answer Yes or No.)

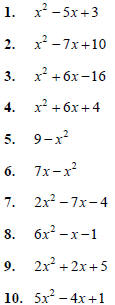
Factor the following polynomials. If the polynomial
can not be rewritten as factors with integer
coefficients, then write the original polynomial as your
answer.

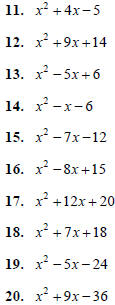
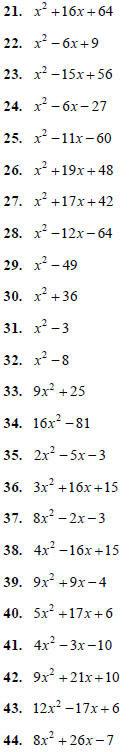
Factor the following. Remember to first factor out the
Greatest Common Factor (GCF) of the terms of the
polynomial, and to factor out a negative if the leading
coefficient is negative.

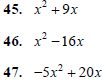
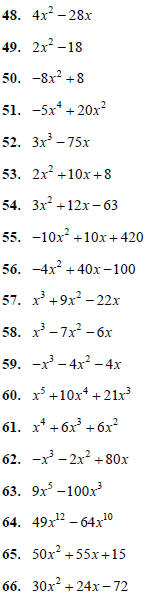
Factor the following polynomials. (Hint: Factor first
by grouping, and then continue to factor if possible.)