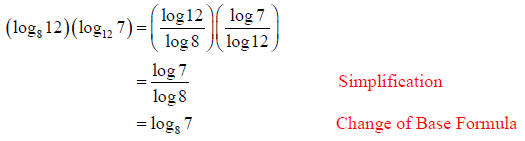Properties of Logarithms
Since the exponential and logarithmic functions with base a are inverse functions, the Laws of Exponents give rise to the Laws of Logarithms.
Laws of Logarithms: Let a be a positive number, with a ≠ 1. Let A > 0, B > 0,
and C be any real numbers.
| Law | Description |
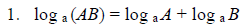 |
The logarithm of a product of numbers is the sum of the logarithms of the numbers. |
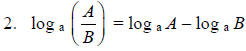 |
The logarithm of a quotient of numbers is the difference of the logarithms of the numbers. |
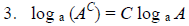 |
The logarithm of a power of a number is the exponent times the logarithm of the number. |
Example 1: Use the Laws of Logarithms to rewrite the
expression in a form with no
logarithm of a product, quotient, or power.
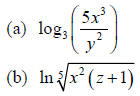
Solution (a):
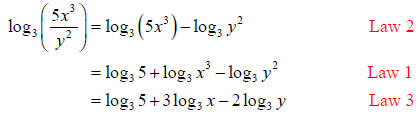
Example 1:
Solution (b):
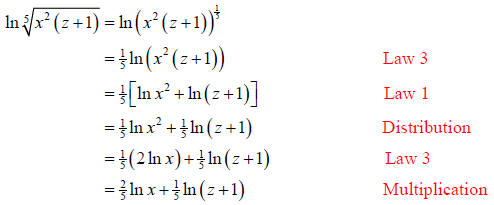
Example 2: Rewrite the expression as a single logarithm.
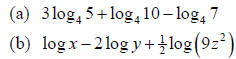
Solution (a):
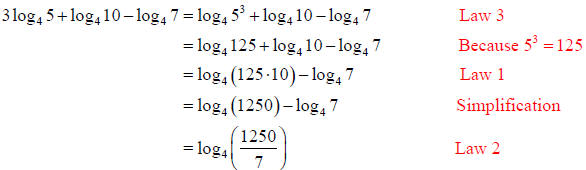
Example 2 :
Solution (b):
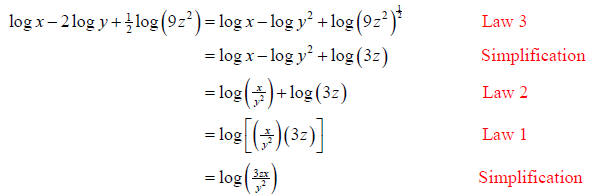
Example 3: Evaluate the expression
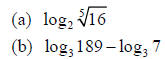
Solution (a):

Solution (b):

Change of Base:
A calculator can be used to approximate the values of common logarithms (base 10) or natural logarithms (base e). However, sometimes we need to use logarithms to other bases. The following rule is used to convert logarithms from one base to another.
Change of Base Formula:
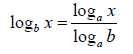
Example 4: Use the Change of Base Formula and a calculator
to evaluate the
logarithm, correct to six decimal places. Use either natural or common
logarithms.
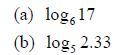
Solution (a):
The Change of Base Formula says
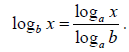
Thus, if we let the new base a = 10
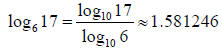
Solution (b):
Again we will use the Change of Base Formula. This time we will let the
new base be a = e.
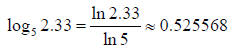
Example 5: Simplify: (log812)(log127)
Solution:
Using the Change of Base Formula with the new base a = 10:
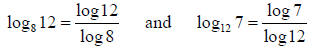
Thus,