Applications of Matrices and Linear Algebra

1 Curves and Surfaces Through Given Points

In this section and the ones that follow, we describe a number of applications of
matrices and linear algebra. Most of these examples come from the text [1]. Other
examples are also available on the web site.

1.1 Two Points on a Line

We are given two points in the plane, say (x₁, y₁) and (x₂, y₂), and we want to find
the equation of the line determined by these two points. Let the equation of the line
be

c₁x + c₂y + c₃ = 0,

where c₁, c₂, and c₃ are to be determined. We write

x₁c₁ + y₁c₂ + 1c₃ = 0,
x₂c₁ + y₂c₂ + 1c₃ = 0,

and

xc₁ + yc₂ + 1c₃ = 0.

Since there is to be a non-trivial solution, the matrix

must have determinant equal to zero. Therefore

x(y₁ − y₂) − y(x₁ − x₂) + (x₁y₂ − x₂y₁) = 0,

and we can choose

c₁ = (y₁ − y₂),
c₂ = (x₂ − x₁),
and
c₃ = (x₁y₂ − x₂y₁).

1.2 A Circle Through Three Given Points

We are given the three non-collinear points (x₁, y₁), (x₂, y₂), and (x₃, y₃) and want to
find the circle containing these points. Any circle in the plane can be described by
an equation of the form

Rewriting this as

we see that the points (x, y) on the circle must satisfy the equation

for some choice of the unknowns c₁, c₂, c₃, and c₄. We write

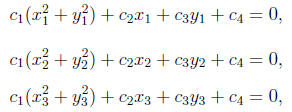
and

Once again, since there is to be a non-trivial solution, the determinant of the matrix

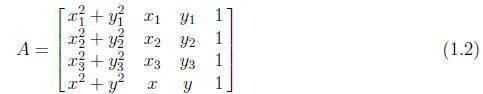
must be zero, and writing this out will give us an equation of the circle in the variables
x and y.

1.3 Additional Examples

The same approach can be used to determine a conic through five points, a plane
through three points, and a sphere through four points.

2 Allocation Problems

We have n different jobs to assign to n different people. For i = 1, ..., n and j = 1, ..., n
the quantity C_ij is the cost of having person i do job j. The n by n matrix C with
these entries is the cost matrix. An assignment is a selection of n entries of C so that
no two are in the same column or the same row; that is, everybody gets one job. Our
goal is to find an assignment that minimizes the total cost

We know that there are n! ways to make assignments, so one solution would be
to determine the cost of each of these assignments and selection the cheapest. But
for large n this is impractical. We want an algorithm that will solve the problem
with less calculation. The algorithm we present here, discovered by two Hungarian
mathematicians in the 1930’s, is called The Hungarian Method.

To illustrate, suppose there are three people and three jobs, and the cost matrix
is

The algorithm is as follows:

• Step 1: Subtract the minimum of each row from all the entries of that row.
This is equivalent to saying that each person charges a certain amount just for
participating, even before any assignments are made, and we must pay these
costs in any case. Subtracting these necessary costs, which do not depend on
the ultimate assignments, cannot change the optimal solutions.
The new matrix is then

• Step 2: Subtract each column minimum from the entries of its column. This
is equivalent to saying that each job has a minimum cost that we must pay,
regardless of who performs it. As before, subtracting these necessary costs does
not change the optimal solutions.
The matrix becomes

• Step 3: Draw a line through the smallest number of rows and columns that
results in all zeros being covered by a line; here I have put in boldface the entries
covered by a line. The matrix becomes

We have used a total of two lines, one row and one column.
What we want is a set of n zeros with the property that each row contains one of
them, and each column contains one of them; we shall call such a set an optimal
set of zeros. Such a set of zeros will provide the desired cheapest assignments.
The next two steps help us decide whether or not such a set of zeros currently
exists.
 

• Step 4: If the number of lines just drawn is n we have finished. In our example,
we are not finished. Proving that needing n lines to cover all the zeros means
that there is an optimal set of zeros is difficult. It is easy to show that if there
exists an optimal set of zeros, then n or more lines are necessary to cover all the
zeros; just notice that any line can contain at most one member of an optimal
set of zeros.

• Step 5: If, as in our example, the number of lines drawn is fewer than n,
determine the smallest entry not yet covered by a line (not boldface, here). It
is 10 in our example. Then subtract this number from all the uncovered entries
and add it to all the entries covered by both a vertical and horizontal line. This
step is equivalent to, first, subtracting the smallest entry from every row not
completely covered by a line, and, second, adding this smallest entry to every
column covered by a line. Since adding or subtracting a fixed amount from any
row or column does not change the optimal solutions, we can return then to
Step 3.

Our matrix becomes

Now return to Step 3.

In our example, when we return to Step 3 we find that we need three lines now
and so we are finished. The optimal allocation is to assign the second person to
the first job, the third person to the second job, and the first person to the third
job. Generally, finding an optimal set of zeros for larger cost matrices, even when we
know such a set must exist, is not a simple matter; there are computer algorithms to
perform this task, however.

Exercise 2.1 Apply this algorithm to the cost matrix

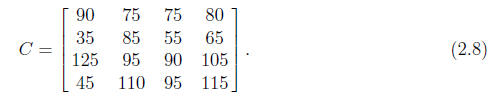
3 Graph Theory

A directed graph is a set of symbols {P₁, P₂, ..., P_n} called the vertices and a set of
ordered pairs (P_i, P_j) for P_i ≠ P_j , called the edges of the directed graph. Write
P_i -> P_j if and only if (P_i, P_j) is an edge. We represent this directed graph using
the matrix M with M_ij = 1 if P_i -> P_j and M_ij = 0 otherwise. See the download
“Motivating Matrix Operations” for a discussion of influence graphs and dominance-
directed graphs.

A subset of vertices is called a clique if and only if it has at least three members,
P_i -> P_j and P_j -> P_i for each pair of vertices in the subset, and we cannot add a
vertex to the subset without violating the second condition. Define a matrix S so
that S_ij = 1 if and only if P_i -> P_j and P_j -> P_i; otherwise S_ij = 0. Then the vertex
P_i is a member of a clique if and only if (S^3)ⁱⁱ ≠ 0.

4 Game Theory

The use of a pay-off matrix in game theory provides a good application of linear
algebra; see the pdf on the web site.

5 Markov Chains

Let {1, 2, ..., k} be states. For i = 1, ..., k and j = 1, ..., k let P_ij ≥ 0 be the probability
of going from state j to state i in one step. The matrix P with entries P_ij is called
the transition matrix. We begin with a column vector , where
is the probability that we start in state i. For n = 1, 2, ... the vector xⁿ is the vector
whose entry 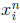is the probability of being in state i after n steps, given the initial
probability vector x^0. We then have

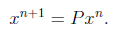
We are often interested in the limiting behavior of the xⁿ.

For example, let

and let x^0 = [1 0]^T . Then for n even we have xⁿ = [1 0]^T and for n odd we have
xⁿ = [0 1]^T .

We say that P is regular if, for some n, the matrix Pⁿ has only positive entries.
A basic theorem in Markov Chains is the following:

Theorem 5.1 If P is regular, then there is a probability vector q = (q₁, ..., q_k), with
all entries positive, such that, as 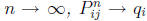for each j. Let Q be the matrix
with Q_ij = q_i, for each i and j.

So the limiting probability of going from j to i is independent of j. For any
probability (column) vector x we have Qx = q. Also Qq = q, so q is an eigenvector
of Q associated with eigenvalue λ = 1.

6 Hill Codes

Simple substitution codes are easily broken by frequency analysis. Here we consider
a code involving matrices.

Number the letters of the alphabet from A = 1 to Y = 25 and Z = 0. To encode
the sentence “I am hiding” , we first group the letters in pairs, as “ia mh id in gg”.
Then replace each letter by its number, to get

9 1, 13 8, 9 4, 9 14, 7 7,

and view each of these pairs of numbers as a two-by one vector. Select an encoding
matrix A; in this case we use a two-by-two matrix

Now multiply each of the two-by-one vectors by A; in our example we get [11 3]^T ,
which is KC, [29 24] = [3 24]^T , which is CX, and so on. This is a Hill-2 cipher. To
decode, we need A to be invertible modulo 26, which means that its determinant,
modulo 26 must have an inverse, modulo 26, which will happen if and only if this
determinant modulo 26 is not divisible by 2 or 13.

Exercise 6.1 Find a decoding procedure for this Hill code by calculating a modulo-26
inverse for the matrix A.