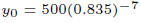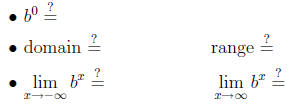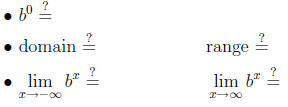Exponential Functions
GOAL: Learn exponential functions with different
bases and use them to model real-world situtations.
Exponential functions are of the form
:
where b > 0 is called base, like f(x) = 2x.
Q1: Where do they appear?
A1: Everywhere! For example, if we put $1 in an account paying 5% interest,
compounded annually,
then t years later it will become f(t) = (1.05)t, which is an exponential
function with base b = 1.05.
The laws of exponents. For b > 0 and u and v any numbers, we have
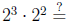
and
and
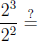
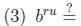for any real number r;
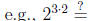and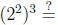 
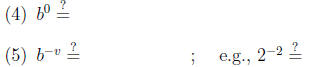
Example 1 If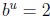 
and
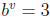then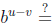 
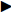Graph of 
| Case 1: b > 1 For example, y = 2x. (i) Complete the table below:
Truncate answers to 2 decimal places
(iii) Properties of bx when b > 1:
• Asymptote: |
Case 2: 0 < b < 1 For example, y = (1/2)x. (i) Complete the table below: 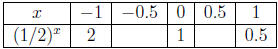 Truncate
answers to 2 decimal places
(iii) Properties of bx when 0 < b < 1:
• Asymptote: |
Three applications of the exponential function
1 Compound interest
Example 1 If $1,000 is invested in an account paying 5% interest, how much will
it grow to in 10 year
if the interest is compounded monthly?
• Annual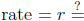 
(in decimals)
• Compounding per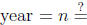 
• Compounding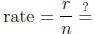 
• Time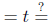
(in years)
At the end of 1st period have:
At the end of 2nd period have:
At the end of 3th period have:
...
At the end of nth period have:
Interest compounded 12 times a year over t years
At the end of 1 year (12 periods) have:
At the end of 2 years (24 periods) have:
...
At the end of t years have:
General formula: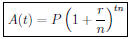 
Example 2 If $8,000 is invested in an account paying 3%
interest, how much will it grow to in 15
years if the interest is compounded quarterly?
2 Population Growth (with unlimited resources)
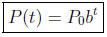
Example 3 A certain bacteria culture grows exponentially. In 1 hour the
population grows from
300,000 to 500,000. Write a formula expressing the population P as a function of
the time t in hours.
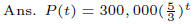
3 Decay of radioactive substances: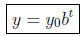 
Example 4 Radon gas decays according to the formula
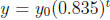, where t is
measured in days.
If there are 500 cubic centimeters left after 7 days, how much was there to
begin with?
